Let’s build open source tensor libraries for data science
Tensor methods for machine learning are fast, accurate, and scalable, but we'll need well-developed libraries.
 Engineers Clean Mirror with Carbon Dioxide Snow (source: NASA Goddard Space Flight Center)
Engineers Clean Mirror with Carbon Dioxide Snow (source: NASA Goddard Space Flight Center)
Data scientists frequently find themselves dealing with high-dimensional feature spaces. As an example, text mining usually involves vocabularies comprised of 10,000+ different words. Many analytic problems involve linear algebra, particularly 2D matrix factorization techniques, for which several open source implementations are available. Anyone working on implementing machine learning algorithms ends up needing a good library for matrix analysis and operations.
But why stop at 2D representations? In a recent Strata + Hadoop World San Jose presentation, UC Irvine professor Anima Anandkumar described how techniques developed for higher-dimensional arrays can be applied to machine learning. Tensors are generalizations of matrices that let you look beyond pairwise relationships to higher-dimensional models (a matrix is a second-order tensor). For instance, one can examine patterns between any three (or more) dimensions in data sets. In a text mining application, this leads to models that incorporate the co-occurrence of three or more words, and in social networks, you can use tensors to encode arbitrary degrees of influence (e.g., “friend of friend of friend” of a user).
Being able to capture higher-order relationships proves to be quite useful. In her talk, Anandkumar described applications to latent variable models — including text mining (topic models), information science (social network analysis), recommender systems, and deep neural networks. A natural entry point for applications is to look at generalizations of matrix (2D) techniques to higher-dimensional arrays. For example, the image that follows is an attempt to illustrate one form of eigen decomposition:

Tensor methods are accurate and embarrassingly parallel
Latent variable models and deep neural networks can be solved using other methods, including maximum likelihood and local search techniques (gradient descent, variational inference, EM). So, why use tensors at all? Unlike variational inference and EM, tensor methods produce global and not local optima, under reasonable conditions. In her talk, Anandkumar described some recent examples — topic models and social network analysis — where tensor methods proved to be faster and more accurate than other methods.

Scalability is another important reason why tensors are generating interest. Tensor decomposition algorithms have been parallelized using GPUs, and more recently using Apache REEF (a distributed framework originally developed by Microsoft). To summarize, early results are promising (in terms of speed and accuracy), and implementations in distributed systems lead to algorithms that scale to extremely large data sets.
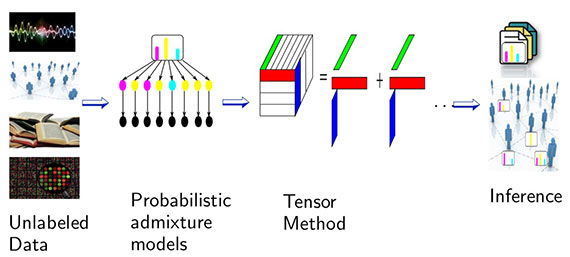
Hierarchical decomposition models
Their ability to model multi-way relationships make tensor methods particularly useful for uncovering hierarchical structures in high-dimensional data sets. In a recent paper, Anandkumar and her collaborators automatically found patterns and “…concepts reflecting co-occurrences of particular diagnoses in patients in outpatient and intensive care settings.”
Why aren’t tensors more popular?
If they’re faster, more accurate, and embarrassingly parallel, why haven’t tensor methods become more common? It comes down to libraries. Just as matrix libraries are needed to implement many machine learning algorithms, open source libraries for tensor analysis need to become more common. While it’s true that tensor computations are more demanding than matrix algorithms, recent improvements in parallel and distributed computing systems have made tensor techniques feasible.
There are some early libraries for tensor analysis in MATLAB, Python, TH++ from Facebook, and many others from the scientific computing community. For applications to machine learning, software tools that include tensor decomposition methods are essential. As a first step, Anandkumar and her UC Irvine colleagues have released code for tensor methods for topic modeling and social network modeling that run on single servers.
But for data scientists to embrace these techniques, we’ll need well-developed libraries accessible from the languages (Python, R, Java, Scala) and frameworks (Apache Spark) we’re already already familiar with. (Coincidentally, Spark developers just recently introduced distributed matrices.)
It’s fun to see a tool that I first encountered in math and physics courses having an impact in machine learning. But the primary reason I’m writing this post is to get readers excited enough to build open source tensor (decomposition) libraries. Once these basic libraries are in place, tensor-based algorithms become easier to implement. Anandkumar and her collaborators are in the early stages of porting some of their code to Apache Spark, and I’m hoping other groups will jump into the fray.
To view Anima Anandkumar’s talk at Strata + Hadoop World in San Jose, Tensor Methods for Large-scale Unsupervised Learning: Applications to Topic and Community Modeling, sign-up for a free trial of Safari Books Online.
