 Rastrigin Function. (source: Diegotorquemada on Wikimedia Commons)
Rastrigin Function. (source: Diegotorquemada on Wikimedia Commons) At the heart of deep learning lies a hard optimization problem. So hard that for several decades after the introduction of neural networks, the difficulty of optimization on deep neural networks was a barrier to their mainstream usage and contributed to their decline in the 1990s and 2000s. Since then, we have overcome this issue. In this post, I explore the “hardness” in optimizing neural networks and see what the theory has to say. In a nutshell: the deeper the network becomes, the harder the optimization problem becomes.
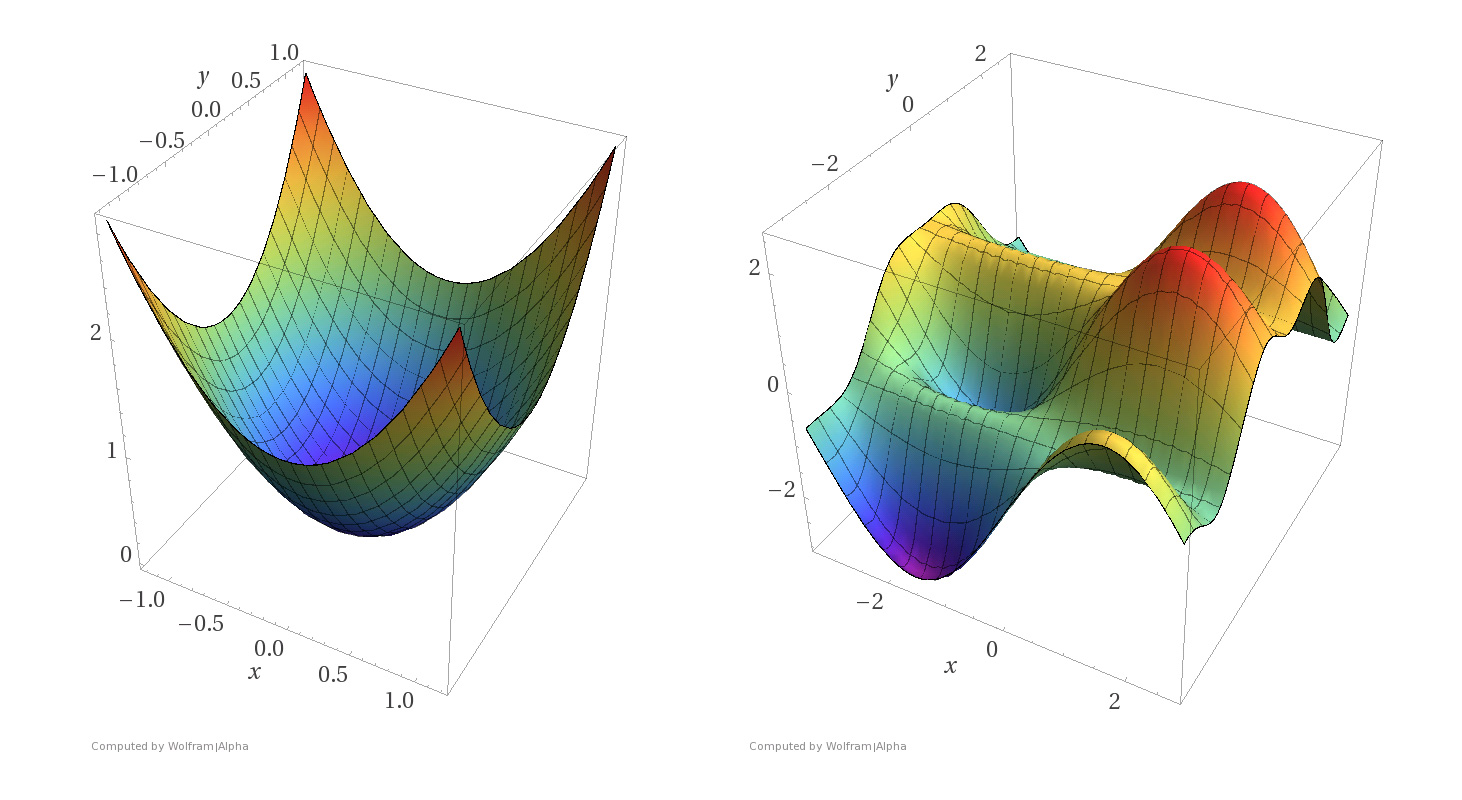
The simplest neural network is the single-node perceptron, whose optimization problem is convex. The nice thing about convex optimization problems is that all local minima are also global minima. There is a rich variety of optimization algorithms to handle convex optimization problems, and every few years a better polynomial-time algorithm for convex optimization is discovered. Optimizing weights for a single neuron is easy using convex optimization (see graphic below). Let’s see what happens when we go past a single neuron.
The next natural step is to add many neurons, while keeping a single layer. For the single-layer, n-node perceptron neural network, if there exist edge weights so that the network correctly classifies a given training set, then such weights can be found in polynomial time in n using linear programming, which is also a special subset of convex optimization. A natural question arises: can we make similar guarantees about deeper neural networks, with more than one layer? Unfortunately not.
To provably solve optimization problems for general neural networks with two or more layers, the algorithms that would be necessary hit some of the biggest open problems in computer science. So, we don’t think there’s much hope for machine learning researchers to try to find algorithms that are provably optimal for deep networks. This is because the problem is NP-hard, meaning that provably solving it in polynomial time would also solve thousands of open problems that have been open for decades. Indeed, in 1988 J. Stephen Judd shows the following problem to be NP-hard:
Given a general neural network and a set of training examples, does there exist a set of edge weights for the network so that the network produces the correct output for all the training examples?
Judd also shows that the problem remains NP-hard even if it only requires a network to produce the correct output for just two-thirds of the training examples, which implies that even approximately training a neural network is intrinsically difficult in the worst case. In 1993, Blum and Rivest make the news worse: even a simple network with just two layers and three nodes is NP-hard to train!
Theoretically, there is contrast of deep learning with many simpler models in machine learning, such as support vector machines and logistic regression, that have mathematical guarantees stating the optimization can be performed in polynomial time. With many of these simpler models, we are able to guarantee you won’t find any better model by running an optimization algorithm longer than polynomial time. But the optimization algorithms that exist for deep neural networks don’t afford such guarantees. You don’t know after you’ve trained a deep neural network whether, given your setup, this is the best model you could have found. So, you’re left wondering if you would have a better model if you kept on training.
Thankfully, we can get around these hardness results in practice very effectively: running typical gradient descent optimization methods gives good enough local minima that we can make tremendous progress on many natural problems, such as image recognition, speech recognition, and machine translation. We simply ignore the hardness results and run as many iterations of gradient descent as time allows.
It seems traditional theoretical results in optimization are heavy-handed—we can largely get past them by way of engineering and mathematical tricks, heuristics, adding more machines, and using new hardware such as GPUs. There is active research into teasing out why typical optimization algorithms work so well, despite the hardness results.
The reasons for the success of deep learning go far beyond overcoming the optimization problem. The architecture of the network, amount of training data, loss function, and regularization all play crucial roles in obtaining leading quality numbers in many machine learning tasks. In future posts, I will address some more modern theoretical results that cover these other aspects, to explain why neural networks work so well on a variety of tasks.
