2
THE FOURIER TRANSFORM
In this section, we develop the Fourier transform and its inverse. The Fourier transform can be thought of as a continuous form of Fourier series. A Fourier series decomposes a signal on [–π, π] into components that vibrate at integer frequencies. By contrast, the Fourier transform decomposes a signal defined on an infinite time interval into a λ-frequency component where λ can be any real (or even complex) number. Besides being of interest in their own right, the topics in this chapter will be important in the construction of wavelets in the later chapters.
2.1 INFORMAL DEVELOPMENT OF THE FOURIER TRANSFORM
2.1.1 The Fourier Inversion Theorem
In this section we give an informal development of the Fourier transform and its inverse. Precise arguments are given in the Appendix (see A.l).
To obtain the Fourier transform, we consider the Fourier series of a function defined on the interval –l ≤ x ≤ l and then let l go to infinity. Recall from Theorem 1.20 (with a = l) that a function defined on –l ≤ x ≤ l can be expressed as
where
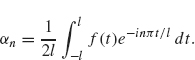
If f is defined on the entire real line, then it is tempting to let l go to infinity and see how the preceding formulas are affected. Substituting the expression for αn into the previous sum, we obtain
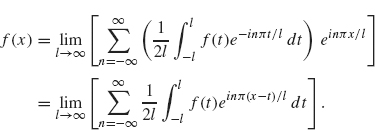
Our goal is to recognize the sum ...

