A First Course in Wavelets with Fourier Analysis, 2nd Edition

7

OTHER WAVELET TOPICS

This chapter contains a variety of topics of a more advanced nature that relate to wavelets. Since these topics are more advanced, an overview will be presented with details left to the various references.

7.1 COMPUTATIONAL COMPLEXITY

7.1.1 Wavelet Algorithm

In this section we briefly discuss the number of operations required to compute the wavelet decomposition of a signal (the computational complexity of the wavelet decomposition algorithm).

To take a concrete setting, suppose f is a continuous signal defined on the unit interval 0 ≤ t ≤ 1. Let

be a discrete sampling of ƒ. We wish to count the number of multiplications in the decomposition algorithm in terms of the number N = 2ⁿ.

The decomposition algorithm stated in Eq. (5.12) or Eq. (5.17) computes the a^j-i and b^j–i, j = n,..., 1, using the formulas

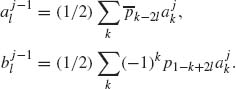
Note that there are half as many a^j-i coefficients as there are a^j coefficients. So the index l on the left runs from 0 to 2^j–

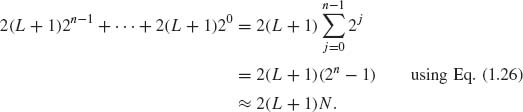
This result is often summarized by stating that the wavelet decomposition algorithm requires O(N) multiplication operations where N is the number of data at the top level. Here, O(N) stands for a number that is proportional to N. The ...