APPENDIX ASUMMARY OF VECTOR/MATRIX OPERATIONS
This Appendix summarizes properties of vector and matrices, and vector/matrix operations that are often used in estimation. Further information may be found in most books on estimation or linear algebra; for example, Golub and Van Loan (1996), DeRusso et al. (1965), and Stewart (1988).
A.1 DEFINITION
A.1.1 Vectors
A vector is a linear collection of elements. We use a lower case bold letter to denote vectors, which by default are assumed to be column vectors. For example,
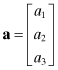
is a three-element column vector. A row vector is (obviously) defined with elements in a row; for example,
A vector is called unit or normalized when the sum of elements squared is equal to 1:
for an n-element vector a.
A.1.2 Matrices
A matrix is a two-dimensional collection of elements. We use bold upper case letters to denote matrices. For example,
is a matrix with two rows and three columns, or a 2 × 3 matrix. Individual elements are labeled with the first subscript indicating the row, and the second indicating the column. An n-element column vector may be ...
