Advances in Applied Mechanics

2.5 Nonslipping Solution for Power-Law-Shaped Indenters

2.5.1 The General Solution

Let us consider in detail the nonslipping contact for punches of monomial shape. In the nonslipping contact problem, the equation for the determination of the derivative of the sought function δ′(t) of displacements under the punch of shape x₃ = −f(r) has the form (Mossakovskii, 1963)

$f\left(r\right)=\frac{2}{\pi }{\displaystyle \underset{0}{\overset{r}{\int }}\frac{1}{\sqrt{r^2-x^2}}\left[{\displaystyle \underset{0}{\overset{x}{\int }}{\delta }^{\prime }\left(t\right)\text{cos}\left(\beta \text{ln}\frac{x-t}{x+t}\right)\text{d}t}\right]\text{d}x}.$

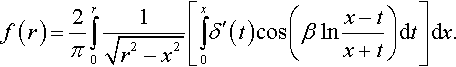  (3.69)

It follows from Eq. (3.69) that if δ′(t) = K_dt^d−1 or δ(t) = K_dt^d/d, then f(r) = B_dr^d, where

$B_d=K_d{C}_d,C_d=\frac{2}{\pi }{I}^{*}\left(d\right)I^{**}\left(d\right),$

  (3.70) ...