Airline Network Planning and Scheduling

17Example on IFAM

17.1 Problem Definition

To further explain the different components of the itinerary‐based fleet assignment model (IFAM) described in the previous chapter, this chapter provides an application of the IFAM considering a small hypothetical airline network. Figure 17.1 shows the flight schedule of this airline, which includes six flights. As shown in the figure, the airline serves three stations: LAX, ORD, and BOS. The six flights are identified as LAX‐ORD (f1), ORD‐BOS (f2), LAX‐BOS (f3), BOS‐ORD (f4), ORD‐LAX (f5), and BOS‐LAX (f6). Thus, city‐pairs LAX‐ORD, ORD‐LAX, ORD‐BOS, and BOS‐ORD are served by nonstop itineraries, and city‐pairs LAX‐BOS and BOS‐LAX are served by nonstop and connecting itineraries.

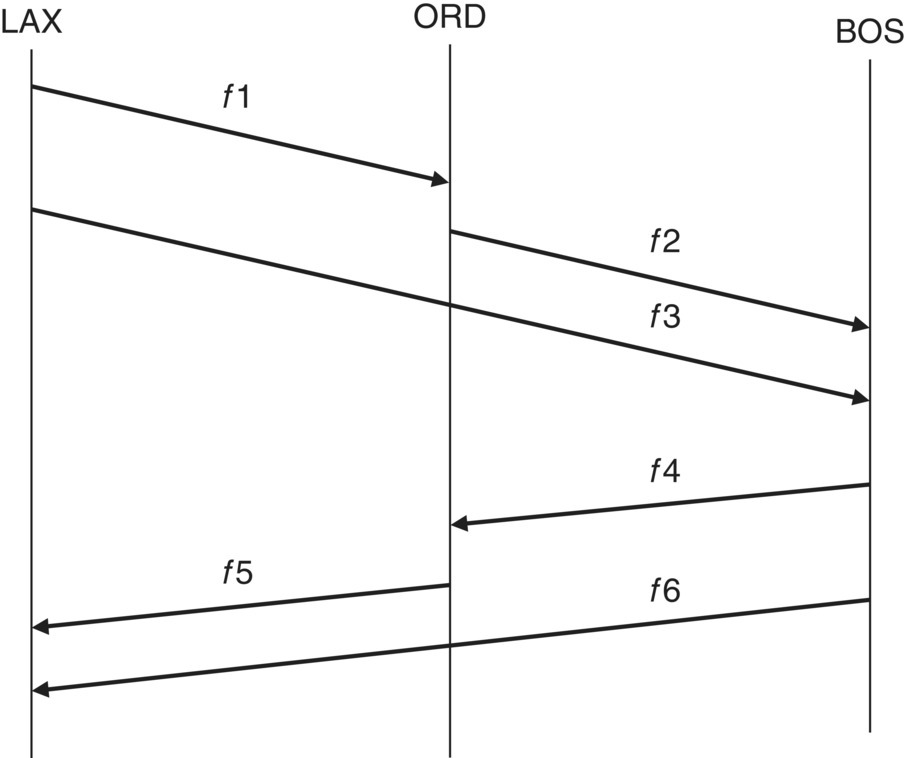
Figure 17.1 An example of a hypothetical airline with six flights for the IFAM problem.

Accordingly, the network includes eight different itineraries, which are LAX‐ORD, ORD‐BOS, LAX‐BOS, BOS‐ORD, ORD‐LAX, BOS‐LAX, LAX‐ORD‐BOS, and BOS‐ORD‐LAX. The demand and average fare value for the eight itineraries are given in Table 17.1. Assume that each of these six flights can be assigned to fleet types e1 or e2 with seat capacity of 150 and 250, respectively. These two fleet types are assumed to have the same speed. Thus, the flight’s arrival time is independent of its assigned fleet type (i.e. identical time‐staggered diagrams and interconnection nodes for the ...