Algebra and Trigonometry, 5th Edition

3.1 The Complex Numbers

• Perform computations involving complex numbers.

Some functions have zeros that are not real numbers. In order to find the zeros of such functions, we must consider the complex-number system.

The Complex-Number System

JUST IN TIME 1

We know that the square root of a negative number is not a real number. For example, $\sqrt{-1}$ is not a real number because there is no real number x such that $x^2=-1$. This means that certain equations, like $x^2=-1$ or $x^2+1=0$, do not have real-number solutions, and certain functions, like $f(x)=x^2+1$, do not have real-number zeros. Consider the graph of $f(x)=x^2+1$.

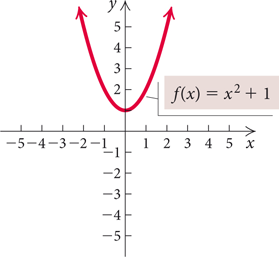
We see that the graph does not cross ...