Chapter 5
![]()
OPTIONS: RISK AND VALUE-AT-RISK
Tt was the increasing use of trading instruments exhibiting non-linear characteristics such as options that was the prime mover behind the development and adoption of value-at-risk type methodologies, as traditional risk measures such as modified duration were deemed to be less and less adequate. This chapter introduces the application of VaR to option instruments. First though, we look at the Black–Scholes option pricing model (B-S model).
OPTION VALUATION USING THE BLACK–SCHOLES MODEL
We begin with a brief overview of the valuation of options. For a basic description of options we recommend Financial Market Analysis by David Blake, while Robert Kolb's Futures, Options and Swaps provides a good description of the B-S model.
Option pricing
The original valuationmodel, and still commonly used in the market for plain vanilla options, was the Black–Scholes model (B-S), which was first presented by its authors in 1973. The basic model is:
![]()
where
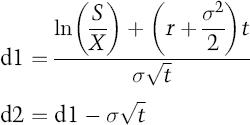
and
| C | is the price of a call option; |
| S | is the current price of the underlying asset; |
| X | is the strike price; |
| r | is the risk-free interest rate; |
| t | is the time to expiry; |
| N(.) | is the cumulative ... |
Get An Introduction to Value-At-Risk, Fourth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

