Analysis of Complex Networks

12.4 A Parameterized Class of Subproblems of the CLC Problem

To perform the complexity analysis of the CLC problem, it is convenient to represent its input in the form of graph Ĝ = (V, C; E, E_A) depicted in Figure 12.2. The set of vertices of this graph consists of two parts: V and C; set V will be referred to as the left part of graph Ĝ, while C will be called the right part. The set of edges will also consist of two parts: E and E_A; the edges from E connect vertices in the left part, while the edges from E_A connect parts V and C (i.e., constitute a bipartite subgraph of Ĝ); an edge (v, i) belongs to E_A iff i ∈ A(v) (i.e., color i is admissible for vertex v).

The complexity of this problem will depend significantly on four parameters of graph Ĝ: T, Δ_V, Δ_V,C, Δ_C,V.

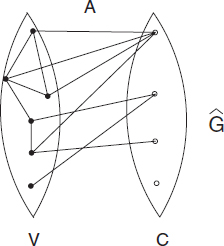
Figure 12.2 Graph Ĝ defining an example of the CLC problem.

The first parameter T defines the type of graph G. We will distinguish between two types of graphs, depending on whether G is acyclic or not. Respectively, T will take only two values: 0 and ∞; T = 0 denotes the case of an acyclic graph G; otherwise T = ∞.

The second parameter Δ_V denotes the maximum vertex degree of graph G (where we take into account only the edges from V to V).

The third parameter Δ_V,C denotes the maximum vertex degree in V with respect to edges from E_A. It corresponds to the maximum cardinality of lists A(v).

Finally, the fourth parameter ...