Analysis of Complex Networks

14.4 Classification of Elementary ({2, 3}, 4)-Polycycles

Theorem 14.4 Any elementary ({2, 3},4)-polycycle is one of the following eight:

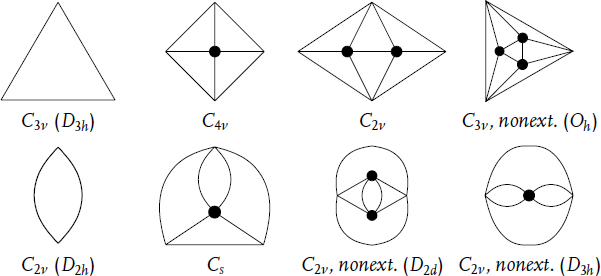
Proof. The list of elementary ({3},4)_simp-polycycles is determined in [3] and consists of the first four graphs of this theorem. Let P be a ({2, 3}, 4)-polycycle containing a 2-gon. If|F₁| = 1, then it is the 2-gon. Clearly, the case where two 2-gons share one edge is impossible. Assume that P contains two 2-gons that share a vertex. Then we should add a triangle on both sides and thus obtain the second polycycle given above. If there is a 2-gon that does not share a vertex with a 2-gon, then P contains the following pattern:

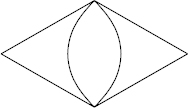
Thus, clearly, P is one of the last two possibilities above.

Note that the seventh and fourth polycycles in Theorem 14.4 are, respectively, 2- and 3-antiprisms; here the exterior face is the unique hole. The m-antiprism for any m ≥ 2 can also be seen as a ({2, 3}, 4)-polycycle with F₂ consisting of the exterior and interior m-gons; this polycycle is not elementary.