Analysis of Complex Networks

17.3 Random Mappings

While in the previous section we considered a particularly simple kind of random graphs, we now turn to slightly more complex graphs. Random mappings are mappings from an n element set M into itself where uniform distribution is assumed. Obviously, any such mapping gives rise to a directed graph: Draw n points in the plane and label them with the elements of M. Then draw a directed edge from i to j (i, j ∈ M) whenever the mapping maps i onto j. This graph is called the functional digraph of the mapping and allows an easy decomposition. Each component contains exactly one cycle (which may be a loop) and to each vertex of the cycle is attached a Cayley tree (i.e., a labeled rooted tree). So a functional digraph decomposes into a multiset of cycles of labeled tree (see Figure 17.2 for an example).

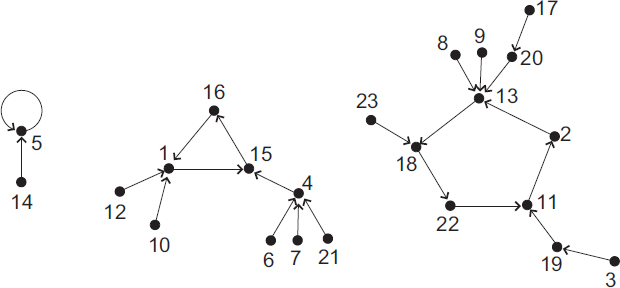
Figure 17.2 A random mapping on M = {1, 2,...,23}.

From this decomposition it is easy to derive the GF for the numbers of such mappings. It is well known (cf. [24]) that the multiset and cycle construction for labeled objects correspond to e^z and log(1/(1 – z)) for the exponential GFs. Hence the exponential GF is

where a(z) is the GF for Cayley trees, given by the functional equation

Of course, elementary enumeration shows that [zⁿ]A(z) = nⁿ/n! such that the above decomposition ...