Analysis of Complex Networks

9.12 Planar Subgraphs

There are two different contexts in which the term planarity can be used. Here we distinguish between chemical planarity and graph planarity. The latter is used for an abstract presentation of chemical compounds in 2D. In accordance with Kuratowski's theorem, graphs that do not have K3,3 and K5 graphs as subgraphs are planar, that is, they can be drawn in 2D without edge intersections (Figure 9.6).

In practice testing a graph against this theorem is considered to be a last choice due to its complexity. The simple test that says that a graph is nonplanar is as follows: given graph G(X,Y), where X is the vertices, Y is the edges, N is the number of vertices, and M is the number of edges, the graph with at least three vertices where M > 3N – 6 is nonplanar. Another test is to see if there are no three member rings and M > 2N − 4. Although all chemical compounds are probably planar in terms of graph theory, they are sometimes classified as 3D to underline essential properties influenced by 3D conformation. As well as aromatic ring systems conjugated bonds in other compounds exhibit chemical planarity. An example is the amide group shown in Figure 9.7.

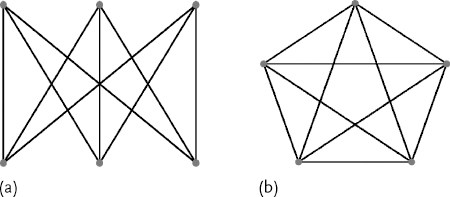
Figure 9.6 (a) K3,3 complete bipartite graph of six vertices three of which connect to each of the other three; (b) K5 complete graph of five vertices.

Figure 9.7 (a) Amide schematic 2D representation; (b) amide ...