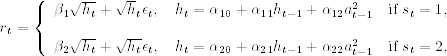Analysis of Financial Time Series, Third Edition

12.9 Markov Switching Models

The Markov switching model is another econometric model for which MCMC methods enjoy many advantages over the traditional likelihood method. McCulloch and Tsay (1994b) discuss a Gibbs sampling procedure to estimate such a model when the volatility in each state is constant over time. These authors applied the procedure to estimate a Markov switching model with different dynamics and mean levels for different states to the quarterly growth rate of U.S. real gross national product, seasonally adjusted, and obtained some interesting results. For instance, the dynamics of the growth rate are significantly different between periods of economic “contraction” and “expansion.” Since this chapter is concerned with asset returns, we focus on models with volatility switching.

Suppose that an asset return rt follows a simple two-state Markov switching model with different risk premiums and different GARCH dynamics:

12.55

where , {ϵt} is a sequence of Gaussian white noises with mean zero and variance 1, and the parameters αij satisfy some regularity conditions so that the unconditional variance of at exists. The probability transition from one state to another is governed by

12.56

where 0 < ei < 1. A small ei means that the return series has a tendency to stay in ...