Applied Cryptography: Protocols, Algorithms, and Source Code in C, Second Edition

CHAPTER 22

Key-Exchange Algorithms

22.1 DIFFIE-HELLMAN

Diffie-Hellman was the first public-key algorithm ever invented, way back in 1976 [496]. It gets its security from the difficulty of calculating discrete logarithms in a finite field, as compared with the ease of calculating exponentiation in the same field. Diffie-Hellman can be used for key distribution—Alice and Bob can use this algorithm to generate a secret key—but it cannot be used to encrypt and decrypt messages.

The math is simple. First, Alice and Bob agree on a large prime, n and g, such that g is primitive mod n. These two integers don't have to be secret; Alice and Bob can agree to them over some insecure channel. They can even be common among a group of users. It doesn't matter.

Then, the protocol goes as follows:

1. (1) Alice chooses a random large integer x and sends Bob

   

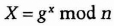
2. (2) Bob chooses a random large integer y and sends Alice

   

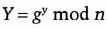
3. (3) Alice computes

   

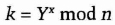
4. (4) Bob computes

   

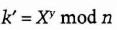
Both k and k are equal to g^xy mod n. No one listening on the channel can compute that value; they only know n, g, X, and Y. Unless they can compute the discrete ...