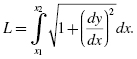Applied Mathematics for Science and Engineering

11An Introduction to the Calculus of Variations and the Finite-Element Method

Some Preliminaries

You may recall that we previously made use of some concepts from the calculus of variations (COV) in our discussion of the variational iteration method (VIM). We will now expand on that very brief treatment to illustrate some other applications of COV. We will mainly follow the conventions employed by Spiegel (1971) and Weinstock (1974). It is important to note that our approach will focus on conservative fields for which the force, F, is related to a potential energy function, ϕ, such that F = −∇ϕ.

Consider a function, y = f(x), in the x-y plane that joins the two points, (x₁, y₁) and (x₂, y₂), together. We recall from elementary calculus that the length of the pathway connecting these two points is

(11.1)

To reveal the nature of the problem we wish to contemplate more clearly, let us select two specific points:

Now suppose the function, f(x), connecting these two points is a straight line:

(11.2)

We want to evaluate L from eq. (11.1), recognizing, of course, that the value produced by eq. (11.2) will be the minimum possible length. But we also want to have a couple of comparisons ...