Automation for Robotics

3

Linear Systems

The study of linear systems [BOU 06] is fundamental for the proper understanding of the concepts of stability and the design of linear controllers. Let us recall that linear systems are of the form:

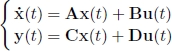
for continuous-time systems and:

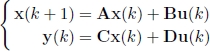
for discrete-time systems.

3.1. Stability

A linear system is stable (also called asymptotically stable in the literature) if, after a sufficiently long period of time, the state no longer depends on the initial conditions, no matter what they are. This means (see Exercises 3.1 and 3.2) that:

In this expression, we can see the concept of matrix exponential. The exponential of a square matrix M of dimension n can be defined through its integer series development:

where I_n is the identity matrix of dimension n. It is clear that e^M is of the same dimension as M. Here are some of the important properties concerning the exponentials of matrices. If 0_n is the zero matrix of n × n and if M and N are two matrices n × n, then:

CRITERION OF STABILITY.– There is a ...