Bayesian Estimation and Tracking: A Practical Guide

2.1 A Very Brief Overview of Matrix Linear Algebra

This section defines notational conventions and matrix operations used throughout the text and provides a brief summary of some matrix linear algebra concepts within the context of MATLAB^®. An extremely good reference for the matrix operations and formulas presented in this section can be found online in Ref. [1].

2.1.1 Vector and Matrix Conventions and Notation

A scalar will usually be presented as lower case, a, a vector as lower case bold, a, and a matrix as upper case bold, A.

An n-vector is the n × 1 column vector

(2.1)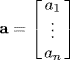

By convention, all vectors will be column vectors. It follows immediately that one can write a column vector as the transpose of a row vector (especially useful to conserve space in a report or journal article)

(2.2)

with commas separating the elements of the vector. represent a vector or matrix transpose, which will be defined below.

An n × m matrix is a two-dimensional array of the form

(2.3)

The first dimension is the number of rows and the second is the number of columns. The ij th component of the matrix ...