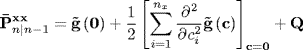7.3 An Alternate Derivation of the Multidimensional Covariance Prediction Equations
For future reference, an alternate set of EKF state covariance prediction equations will be derived here. In the next chapter, these will be turned into finite difference solutions that are used to show the relationship between the finite difference method and the unscented Kalman filter. For numerical integration methods other than the finite difference methods, this is the preferred method for evaluating covariance integrals.
Define the matrix
Now (7.34) can be rewritten as
(7.68) ![]()
This has the exact same form as the state prediction equation (5.51), resulting in
where ![]() has been used to distinguish this form from (7.41).
has been used to distinguish this form from (7.41).
Similarly, the observation covariance prediction becomes
(7.70) 
where
(7.71) ![]()
The cross-covariance matrix prediction equation (5.41) can be transformed into
(7.72)
where ...
Get Bayesian Estimation and Tracking: A Practical Guide now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.