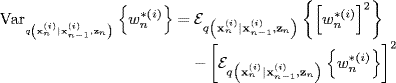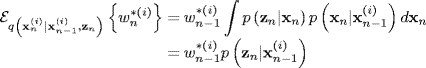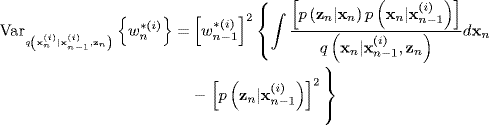Bayesian Estimation and Tracking: A Practical Guide

16.4 The Optimal SIS Particle Filter

To overcome some of the problems of the BPF, one needs to choose the importance density more wisely. Thus, the choice of an importance density is the most critical issue in the design of a particle filter. The optimal choice for an importance density is to choose one that minimizes the variance of the weights. Consider the mean and variance of the weights as follows:

(16.22)

(16.23)

If we first examine the mean equation (16.22), substitution of ((16.12), the recursion equation for results in

(16.24)

Using the same procedure on the first term in the variance equation (16.23) and using (16.24) to evaluate the second term in (16.23), we obtain

(16.25)

It follows immediately from Bayes' law that (16.25) reduces identically to zero [13] if

(16.26)

(16.27)

Now, the expression for the importance weight update (16.12) becomes

(16.28)

(16.29)

Comparing ...