BOND MATH: The Theory Behind the Formulas

The Relationship between Yield Duration and Maturity

An interesting property of Macaulay duration is revealed by letting N, the number of periods to maturity, get large and approach infinity. In equation 6.15, the general expression in equation 6.13 is simplified to apply to a coupon date (i.e., t/T = 0).

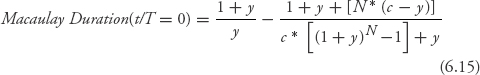
As N approaches infinity, the denominator in the second term gets larger faster than the numerator because N is an exponent in the former and a coefficient in the latter. That whole second term goes to zero and the Macaulay duration becomes just (1+y)/y. Such bonds, known as perpetuities, are rare but do exist. For instance, in the U.K. bonds ...