Classical Geometry: Euclidean, Transformational, Inversive, and Projective

CHAPTER 13

INTRODUCTION TO INVERSIVE GEOMETRY

13.1 Inversion in the Euclidean Plane

We introduce the concept of inversion with a simple example, that of constructing the midpoint of a line segment using only a compass.

Example 13.1.1. Given a line through A and B, find the midpoint of the segment AB using only a compass.

Solution. With center A and radius r = AB, draw the circle C(A, r) and locate the point P on the line AB so that B is the midpoint of AP.

With center P, draw the circle C(P, AP) intersecting the first circle at C, as in the figure on the following page.

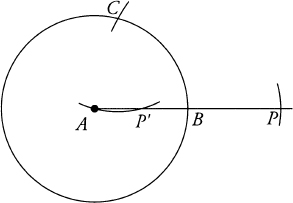
Finally, draw C(C, r) intersecting the line AB at P′. Then P′ is the midpoint of AB.

To sec that this is the case, note that the triangles AP′C and ACP are similar isosceles triangles since they share a vertex angle at A, so that

which implies that

and this implies that

Note that with

we have AP · AP′ = r². This relationship between P and P′ is called an inversion. More generally, we have the following definition: ...