Codecharts: Roadmaps and blueprints for object-oriented programs

Appendix II

Formal Definitions

The secret of being boring is to say everything.

—Voltaire

For notational conventions please refer to page 168.

Definition I. A finite structure is a pair such that:

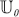• is a set of primitive elements or entities of dimension 0 called the universe of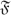
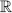• is a finite set of relations (Definition II)

Definition II. A unary (binary) relation is a set of 1-tuples [2-tuples, or pairs] of entities of dimension 0. A class (method, signature) of dimension 0 is an entity in the relation Class (Method, Signature). A class (method, signature) of dimension d is a set of classes (methods, signatures) of dimension d – 1.

Definition III. Given a binary relation BinaryRelation, the transitive closure of BinaryRelation, written BinaryRelation⁺, is that set of pairs x, y such that at least one of the following conditions hold:

• x, y ∈ BinaryRelation
• There exists an element z in ...