College Algebra, 4th Edition

Applying the Concepts

1. 87.

   1. $C(x)=0.5x+2000$

   2. $\overline{C}(x)=0.5+{\displaystyle \frac{2000}{x}}$

   3. $\overline{C}(100)=20.5,$ $\overline{C}(500)=4.5,\overline{C}(1000)=\mathrm{2.5.}$ These show the average cost of producing 100, 500, and 1000 trinkets, respectively.

   4. Horizontal asymptote: $y=0.5.$ It means the average cost (the fixed daily cost of producing each trinket) if the number of trinkets produced approaches $\infty$.

2. 89.

   1. 

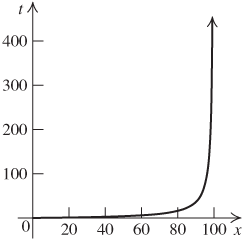
   2. 1. About 9 min

      2. About 12 min

      3. About 76 min

      4. 397 min

   3. 1. $\infty$;

      2. Not applicable; the domain is $x<100$.

   4. No

3. 91.

   1. $3.02 billion

   2. 

   3. 90.89%

4. 93.

   1. 16,000

   2. The population will stabilize at 4000.

5. 95.

   1. $f(x)=(10x+200,\mathrm{000\; ...}$