Corporate and Project Finance Modeling

Chapter 21Constructing Probability Distributions with Trends, Mean Reversion, Price Boundaries, and Correlations among Variables

This chapter turns to more complex aspects of time series models that include parameters for time trends, mean reversion, lower and upper boundaries, jump processes, and correlations. The time series equation introduced in Chapter 20 that only has a volatility parameter would not generally be appropriate for use in financial models. That equation assumed a normal distribution of random numbers, no mean reversion, no upper or lower price boundaries, and no interdependence between different variables. Actual time series equations for financial models should be more complex because representation of real variables generally include added parameters (trends, boundaries, jumps, and so forth), because of transformation to logarithms, and because the random draws may be filtered through a probability distribution other than the normal distribution. A more representative time series equation (without jumps, price boundaries, or correlations, and not in logs) could be written as:

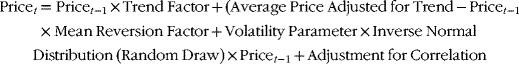
While this equation is more complex than the basic equation that only had volatility, no matter how the time series equation is specified and no matter what probability distribution is used, the process always boils down to the idea of drawing a random number, adjusting it for volatility, ...