Critical Infrastructure Protection in Homeland Security: Defending a Networked Nation, 2nd Edition

Appendix CMath: Spectral Radius

Networks are represented inside of a computer as a matrix. Computer algorithms can then calculate degree, betweenness, cluster coefficient, and spectral radius. (For a more detailed explanation of these algorithms, consult Lewis, T. G. Network Science: Theory and Applications, Hoboken: John Wiley & Sons, Inc., 2009.) This appendix surveys the basics.

C.1 Network as Matrix

Nodes and links are represented internally as a square connection matrix C of dimension n, where n is the number of nodes in the network. Figure C.1 illustrates the correspondence between the flow network of Chapter 4 and its connection matrix. As illustrated in Figure C.1, the rows and columns of C can be labeled with the network's nodes for clarity. The elements are either 0 or 1. If a link exists between node n_i and n_j, a one is placed in the cell corresponding to element (i, j). Otherwise, the cell is zero. Note that i and j start at zero, so they are in [0, n − 1].

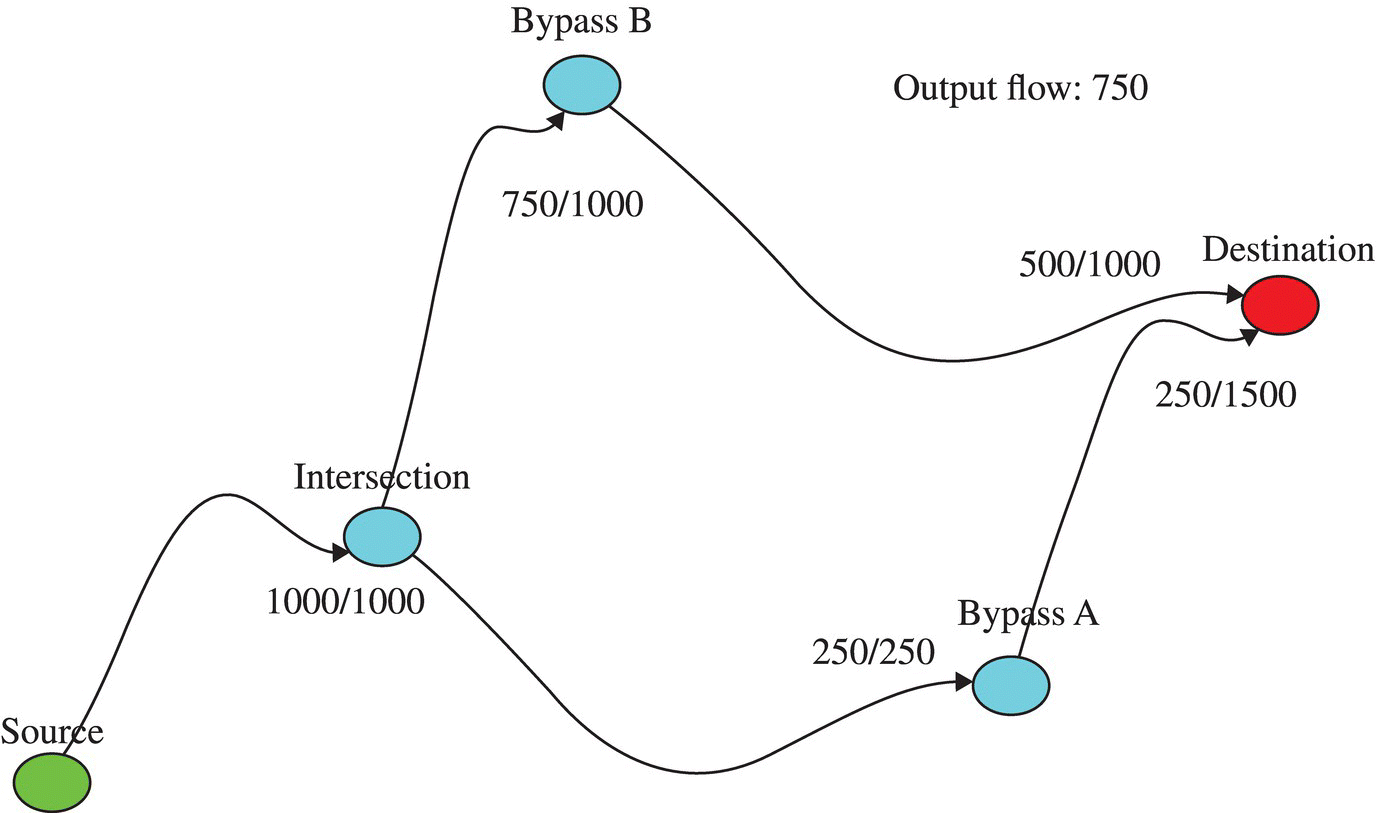
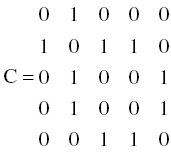
Figure C.1 The flow network of Chapter 4 as it is represented in a computer as a connection matrix (also, see Fig. 4.13 of Chapter 4).

The degree of a node is the sum of its row cells. For example, in Figure ...