Chapter 3
Spectral Observation
The purpose of this chapter is to introduce the reader to the two following fundamental concepts:
3.1 Spectral accuracy and resolution
3.1.1 Observation of a complex exponential
To illustrate the DFT’s use in signal spectrum observation, we will begin with a simple example.
EXAMPLE 3.1 (Sampling a complex exponential)
Consider the sequence resulting from the sampling of a complex exponential e2jπF0t at a frequency of Fs = 1/Ts. If we set f0 = F0/Fs and assume it to be < 1/2, we get x(n) = e2jπf0n.
(3.1) 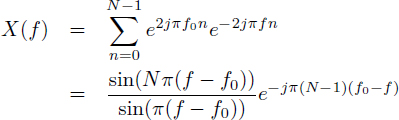
Get Digital Signal and Image Processing using MATLAB, Volume 1: Fundamentals, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

