12.1. Theoretical background
In many classification problems, salient features may be searched and extracted from the time-frequency plane. This process is optimized if the time-frequency representation (TFR) is matched to the processed signal.
For simple signals, the matched TFR may be one of the Cohen's class representations. For more complicated signals the construction of the matched TFR is a difficult problem, since the standard kernels do not preserve some properties required by the optimization procedure.
This chapter deals with some recently proposed approaches for constructing the matched TFR corresponding to a given signal. The optimization procedure aims to cancel the interference terms and to obtain the best time-frequency resolution (in an equivalent manner to the chirp representation with the Wigner-Ville distribution).
12.1.1. Fractional Fourier transform
The a-order fractional Fourier transform (FRFT) is defined, for 0<|a|<2, by means of its kernel:
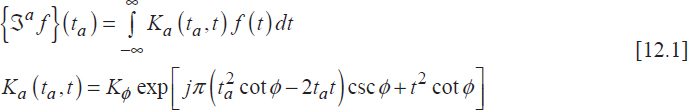
where ![]() = aπ/2 and
= aπ/2 and ![]() = exp[–j(πsgn(
= exp[–j(πsgn(![]() )/4–/2)]/|sin()|0.5.
)/4–/2)]/|sin()|0.5.
For a = 0 and a = ±2 the kernel Ka(ta, t) is defined by K0(ta, t) = ...
Get Digital Signal Processing Using Matlab now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

