Digital Signal Processing Using Matlab

13.3. Exercises

EXERCISE 13.5.

a. Generate two sets of 100 three-dimensional Gaussian vectors having the following mean vector and covariance matrix:

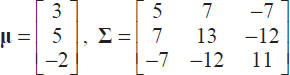
b. Perform the principal component analysis on the first set and then use the obtained result to project the second set. Conclude on the generalization capability of this type of analysis.

c. Repeat the previous analysis after preprocessing the generated vectors, so that the mean of each component is 0 and its standard deviation is 1. Compare to the results previously obtained and conclude about the role of this data preprocessing.

EXERCISE 13.6.

Generate two classes of 500 vectors uniformly distributed inside a sphere of radius 0.3 (first class) and inside a spherical calotte whose radius varies from 0.7 to 1 (second class). The two classes are centered at the origin.

Project the two classes in a two-dimensional space using the PCA, the LDA and the Sammon method randomly initialized. Then repeat the projection using the Sammon algorithm initialized with the PCA solution and conclude on the obtained results.

Use the function below to perform the projection according to the Sammon method.

 function [matr_proj,Sammon_stress,esr_vect]=Sammon_method(matr_init,matr_proj_init, alpha,threshold) % Non-linear projection using the Sammon method %[matr_proj,Sammon_stress,esr_vect]=Sammon_method(matr_init,matr_proj_init, alpha,threshold); % matr_init ...