Discrete Stochastic Processes and Optimal Filtering

1.7. Exercises for Chapter 1

Exercise 1.1.

Let X be an r.v. of distribution function

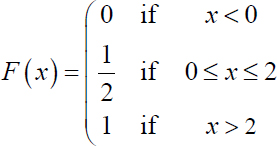
Calculate the probabilities:

Exercise 1.2.

Given the random vector Z = (X,Y) of probability density 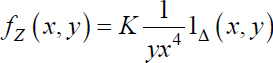where K is a real constant and where 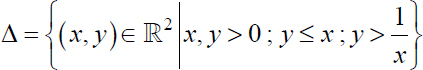, determine the constant K and the densities f_X and f_Y of the r.v. X and Y.

Exercise 1.3.

Let X and Y be two independent random variables of uniform density on the interval [0,1]:

1) Determine the probability density f_Z of the r.v. Z = X + Y;

2) Determine the probability density f_U of the r.v. U = X Y.

Exercise 1.4.

Let X and Y be two independent r.v. of uniform density on the interval [0, 1]. Determine the probability density f_U of the r.v. U = X Y.

Solution 1.4.

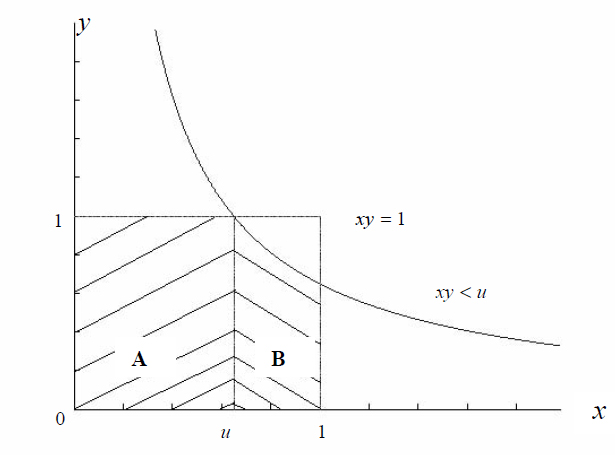
U takes its values in [0,1]

Let F_U be the distribution function of U:

– if u ≤ 0 F_U (u) = 0; if u ≥ 1 F_U (u) = 1;

– if

where is the cross-hatched area of the figure.

Thus

Finally

Exercise 1.5.

Under consideration ...