Engineering Mathematics, Volume 2

1

Eigenvalues and Eigenvectors

1.1 Introduction

In this chapter we will consider polynomials whose coefficients are not real numbers but n-square matrices, find eigenvalues and eigenvectors of a matrix, state and prove an important theorem known as the Cayley–Hamilton Theorem and see how it can be used to find powers of square matrices and inverses of nonsingular matrices.

1.1.1 Matrix Polynomial

If P₀, P₁, …, P_m (≠ 0) are n-square matrices, then an expression of the form

 

 

is called a matrix polynomial of degree ‘m’.

E.g.

 

 

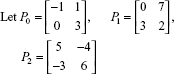
Then

 

 

is ...