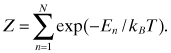Engineering Quantum Mechanics

2

Basic Quantum Statistical Mechanics

2.1 ELEMENTARY STATISTICAL MECHANICS

If a system in equilibrium can be in any of N states, then the probability of the system having energy is given by , where the partition function Z is defined by [1]

(2.1)

Here, is a Boltzmann constant, and T is a temperature. For quantum mechanical system of states , where denotes the state with energy , the expected value of the quantum mechanical operator A is defined by

(2.2)

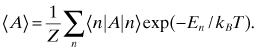
This fundamental law is the essence of statistical mechanics, with the concept of thermal equilibrium and temperature. If a system is very weakly coupled to a heat bath at a given temperature, if the coupling is indefinite or not known ...