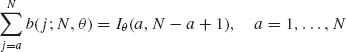Examples and Problems in Mathematical Statistics

CHAPTER 2

Statistical Distributions

PART I: THEORY

2.1 INTRODUCTORY REMARKS

This chapter presents a systematic discussion of families of distribution functions, which are widely used in statistical modeling. We discuss univariate and multivariate distributions. A good part of the chapter is devoted to the distributions of sample statistics.

2.2 FAMILIES OF DISCRETE DISTRIBUTIONS

2.2.1 Binomial Distributions

Binomial distributions correspond to random variables that count the number of successes among N independent trials having the same probability of success. Such trials are called Bernoulli trials. The probabilistic model of Bernoulli trials is applicable in many situations, where it is reasonable to assume independence and constant success probability.

Binomial distributions have two parameters N (number of trials) and θ (success probability), where N is a positive integer and 0 < θ < 1. The probability distribution function is denoted by b(i; N, θ) and is

(2.2.1)

The c.d.f. is designated by B(i; N, θ), and is equal to B(i; N, θ) =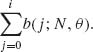

The Binomial distribution formula can also be expressed in terms of the incomplete beta function by

(2.2.2)

where

(2.2.3)

The parameters p and q