Feedback Control for Computer Systems

Chapter 20. The Transfer Function

As Chapter 3 demonstrated, understanding a system’s dynamic behavior is important for building a stable and well-performing feedback loop. In this chapter, we will first describe how to capture information on a system’s dynamic behavior; we then show how to repackage this information in a way that is particularly convenient for our purposes. The tool that we will use is the transfer function.

Differential Equations

The usual way to describe the time evolution of a system is through differential equations. A differential equation is an expression involving the derivative of a quantity, often together with the quantity itself. Here are some examples of differential equations:

 

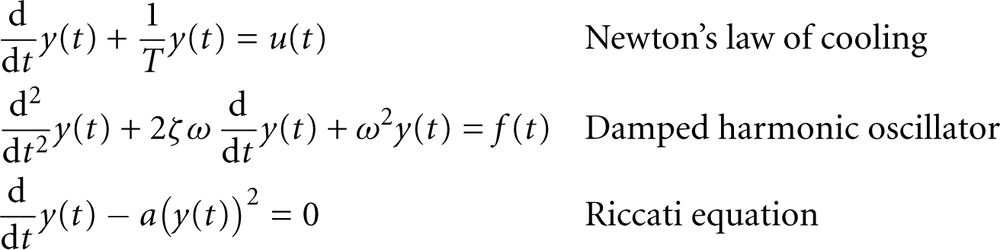
Because the derivative is the rate of change of the quantity, differential equations are the natural way to describe how a system changes over time: they describe the system’s dynamics. “Solving” a differential equation means finding a curve y(t) that, for all times t, fulfills the differential equation. Several analytical and numerical methods exist to find the solution to a given differential equation.

Laplace Transforms

Differential equations provide an especially compact way of describing the dynamics of a system: all possible trajectories, for all times t, can be obtained from the differential equation alone.^[21] We now repackage this information in a way that makes it easier ...