Financial Derivative and Energy Market Valuation: Theory and Implementation in MATLAB

Chapter 13: Fundamentals of Characteristic Functions

13.1 Introduction

Various transforms and generating functions are available in statistics and finance with their particular use based on convenience to the particular application. In this chapter, the characteristic function, which is an alternate form to the probability and cumulative distribution functions for expressing the distribution of a random variable, is introduced.

13.2 Characteristic Function

The characteristic function is simply the Fourier transform of the real-space probability density function as given by

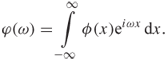
As expected, the inverse Fourier transform of the characteristic function gives the probability density function,

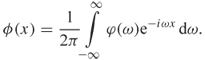
By definition of the Fourier transform, the characteristic function contains the same information as the probability density function. The characteristic function is viewed as the expected value of , which is given by

where is a scalar random variable.

When is a -dimensional random variable, the characteristic ...