Financial Economics

WEB–APPENDIX P

PRINCIPAL COMPONENT ANALYSIS IN FINANCE

In Chapter 15, we discussed principal component analysis (PCA). This statistical tool is widely used in finance. It is useful not only for estimating factor models here, but also for extracting a few driving variables out of many for the covariance matrix of asset returns. Hence, it is important to understand the statistical intuition behind it. To this end, we provide a simple introduction in this appendix.

Perhaps the best way to understand PCA is to go through an example in detail. Suppose there are two risky assets, whose returns are denoted by and , with covariance matrix:

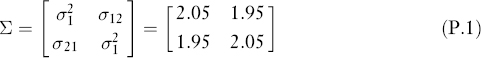
That is, we assume that they have the same variances of 2.05 and covariance of 1.95. Our objective is to find a linear combination of the two assets so that it has a large component in the covariance matrix, as will be clear below. For notational brevity, we assume first that the expected returns are zeros, that is,

and will relax this assumption at the end of this section.

Recall that we call any vector (a₁, a₂)′ satisfying:

an eigenvector of σ, and the ...