Financial Instrument Pricing Using C++, 2nd Edition

CHAPTER 15Univariate Statistical Distributions

15.1 Introduction, Goals and Objectives

In this chapter we give an introduction to univariate statistical distributions, their properties and some initial applications. We focus on the C++ <random> library and the Boost Statistics library. The advantage of this approach in our opinion lies in the fact that we use standardised and de-facto standard libraries. The main topics are:

• How C++ and Boost support univariate distributions.
• Black–Scholes–Merton option pricing using the C++11 error function. Computing option sensitivities.
• Generating input data to numerical processes using random number generators.
• Creating generic classes to encapsulate functionality across a wide range of distribution types in both <random> and Boost.

Much of the flexibility of the code can be attributed to features that C++ supports, for example variadic parameters, tuples and template–template parameters. We also introduce the Command design pattern (GOF, 1995) in the context of callback functions and event triggering mechanisms.

15.2 The Error Function and its Universality

The error function (also called the Gaussian error function) is defined by:

(15.1)

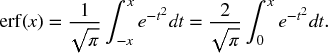
In statistics this function has the following interpretation: let X be a normally distributed random variable with mean 0 and variance 1/2. Then erf(x) describes the probability of X falling in the ...