Financial Instrument Pricing Using C++, 2nd Edition

CHAPTER 16Bivariate Statistical Distributions and Two-Asset Option Pricing

16.1 Introduction and Objectives

In this chapter we continue our discussion of statistical distributions that we introduced in Chapter 15. We create efficient algorithms to compute the cumulative bivariate normal distribution (BVN) function defined by:

(16.1)

where in this case:

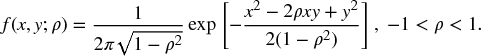
This distribution has many applications and our interest is in using it to price options on two assets (see, for example, Haug, 2007). Contrary to the univariate case there seems to be little software available to compute bivariate distributions and in these cases we resort to a combination of third-party libraries and proprietary code. We propose a number of alternatives and the final choice will be determined by a number of requirements such as efficiency, accuracy, robustness and maintainability:

• S1: The Drezner method (Drezner, 1978).
• S2: The Genz method (Genz, 2004) and its implementation in Quantlib (www.quantlib. org) and by West (West, 2004).
• S3: The formula 26.3.3 in Abramowitz and Stegun (1965) in combination with a Gauss–Legendre numerical quadrature scheme.
• S4: Converting the two-dimensional integral (16.1) defining the cumulative bivariate normal distribution into a hyperbolic PDE that we approximate using the ...