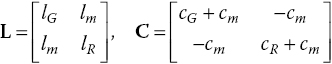Foundations of Electromagnetic Compatibility with Practical Applications

1Matrix and Vector Algebra

Matrices and determinants are very powerful tools in circuit analysis and electromagnetics. Matrices are useful because they enable us to replace an array of many entries as a single symbol and perform operations in a compact symbolic form.

We begin this chapter by defining a matrix, followed by the algebraic operations and properties. We will conclude this chapter by showing practical EMC‐related applications of matrix algebra.

1.1 Basic Concepts and Operations

A matrix is a mathematical structure consisting of rows and columns of elements (often numbers or functions) enclosed in brackets (Kreyszig, 1999, p. 305).

For example,

(1.1)

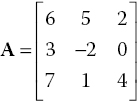
The entries in matrix A are real numbers. Matrices L and C in Eq. (1.2) are the matrices containing per‐unit‐length inductances and capacitances, respectively, representing a crosstalk model of transmission lines (Paul, 2006, p. 567). (We will discuss the details of this model later in this chapter.)

(1.2)

We denote matrices by capital boldface letters. It is often convenient, especially when discussing matric operations and properties, to represent a matrix in terms of its general entry in brackets:

(1.3)

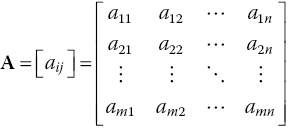
Here, A is an m × n matrix; that ...