FX Options and Smile Risk

2

Pricing Models for FX Options

2.1 PRINCIPLES OF OPTION PRICING THEORY

We will shortly review the theory of option pricing with a strict reference to the FX world. First, we introduce a (slightly extended) BS economy, then we relax one of the basic assumptions: we will allow the volatility of the FX rate process to be stochastic. These principles will pave the way to the analysis of some well-known models employed in practice to price FX options.

2.1.1 The Black-Scholes economy

We work in continuous time and assume that W_t is a standard Brownian motion, and a martingale with respect to a filtered probability space (Ω, Ƒ, F, P ) for the time set [0, ∞). We assume also that the filtration F satisfies the usual conditions,⁸ and that we have a perfect frictionless market, with one domestic and foreign interest rate (at which interest accrues continuously). In the economy, one risky asset is traded: an FX pair whose price process is the following stochastic differential equation (SDE):

(2.1)

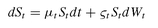where µ_t and ς_t are time-dependent parameters. A second traded asset is a riskless (domestic) deposit,⁹ whose price changes according to the following differential equation:

(2.2)

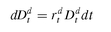An FX pair can be considered as an asset yielding a continuous cash flow equal to the foreign interest rate. In fact, ...