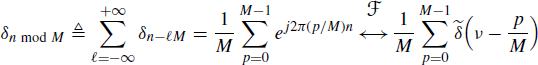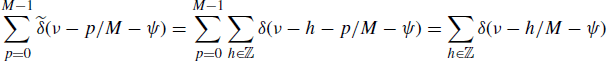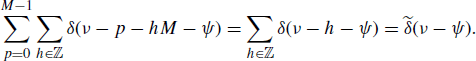Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications

5.11 Proofs for Section 4.10 “Multirate Processing of Discrete-Time Jointly SC Processes”

In this section, proofs of results of Section 4.10 are reported.

For future reference, let us consider the discrete-time sample train with sampling period M, its discrete Fourier series (DFS), and its Fourier transform:

(5.190)

where δ_m is the Kronecker delta, that is, δ_m = 1 if m = 0 and δ_m = 0 if m ≠ 0 and mod M denotes modulo operation with values in {0, 1, …, M − 1}. Thus, δ_{n mod M} = 1 if n = kM for some integer k and δ_{n mod M} = 0 otherwise.

Furthermore, in the sequel, the following identities are used

(5.191)

(5.192)

In the following proofs, the bounded variation assumption (4.192) allows to use the Fubini and Tonelli theorem (Champeney 1990, Chapter 3) to interchange the order of the integrals in ν₁ and ν₂.

5.11.1 Expansion (Section 4.10.1): Proof of (4.241), (4.242b), and (4.242c)

From the identity

(5.193)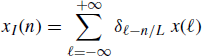

it follows that the impulse-response function of the LTV system that operates expansion is

(5.194)

Thus, the transmission function is

(5.195)

where in the last equality the Poisson's ...