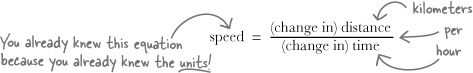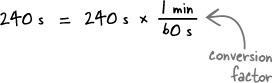Chapter 4. Equations and Graphs: Learning the lingo
Communication is vital. You’re already off to a good start in your journey to truly think like a physicist, but now you need to communicate your thoughts. In this chapter, you’re going to take your first steps in two universal languages - graphs and equations - pictures you can use to speak a thousand words about experiments you do and the physics concepts you’re learning. Seeing is believing.
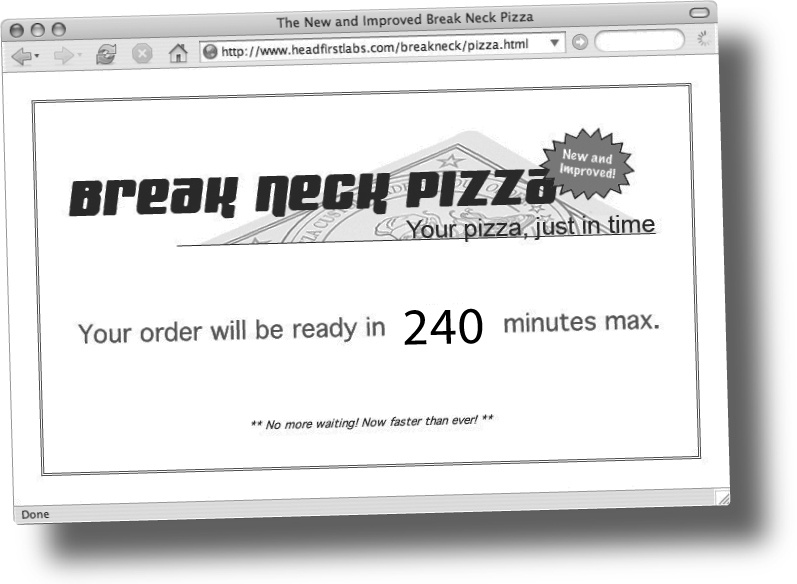
The new version of the Break Neck Pizza website is nearly ready to go live ...
Break Neck Pizza already revolutionized pizza delivery through its patented “just in time” cooking process and its large fleet of delivery bicycles.
But now it’s even better! The award-winning Break Neck website has just been upgraded to give each customer a delivery time for their order.
...but you need to work out how to give the customer their delivery time
You’ve been called in to figure out what time the website should quote each customer. The web programmers are happy to implement your solution, and you also have Alex, the top Break Neck delivery guy, on hand to help. He knows how long it takes him to get to some houses, but you’ll need another way to work out the delivery time to new, unknown neighborhoods.
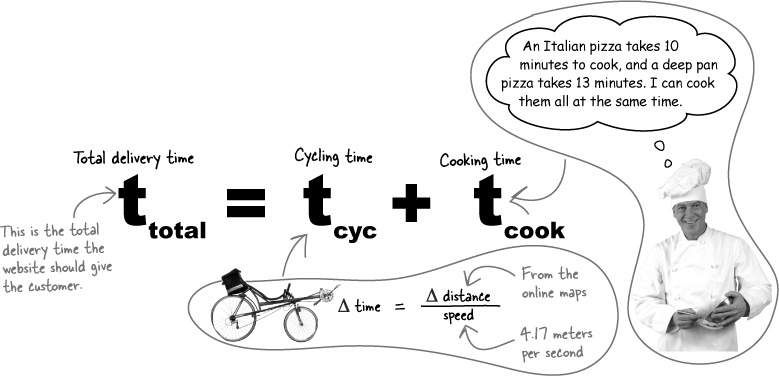
If you write the delivery time as an equation, you can see what’s going on
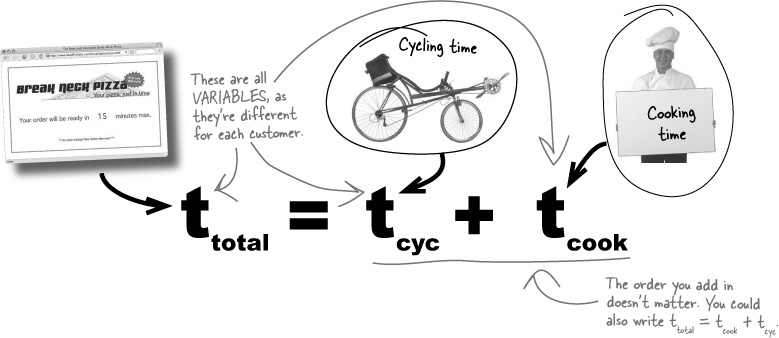
The total delivery time is the time Alex spends cycling to the customer’s house plus the cooking time for the pizza.
It takes a lot of words to describe this, and it’s difficult to tell what’s going on without reading the whole thing. This is why in physics, people use equations to describe how the world works.
You can use letters with subscripts as symbols to represent each of the times:
ttotal for the total delivery time.
tcyc for Alex’s cycling time.
tcook for the cooking time.
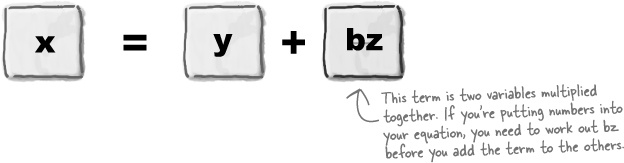
Then you can write down the equation ttotal = tcyc + tcook . This says exactly the same thing as “The total delivery time is equal to the time Alex spends cycling to the customer’s house plus the cooking time for the pizza.” Except the equation lets you see that at a glance.
Equations let you represent the real world symbolically.
Use variables to keep your equation general
An equation like ttotal = tcyc + tcook is general because it isn’t tied to any particular values for the cycling or cooking times. This means you can use the same equation for any order. Any quantity represented by a letter rather than a number is called a variable. Here it’s good for ttotal, tcyc , and tcook to be variables because their values will vary for each customer.
An equation uses symbols to show you that two things are equal to each other.
An equation must have an equal sign!
In an equation, each of the blocks you add together or subtract from each other is called a term. A term can be a number, a single variable, or several numbers and variables multiplied or divided by each other.
A TERM is one of the building blocks that you add or subtract.
You can break down equations by thinking about them one term at a time. If a term is more complicated than a single variable, you need to do all the calculations (multiplying, dividing, and so forth) within a term before you add it to or subtract it from other terms. So that you can spot terms easily, it’s usual to use a shorthand for multiplication, like bz instead of b × z since this groups together all the variables in each term.
Think about equations one term at a time
You need to work out Alex’s cycling time
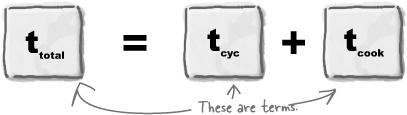
Your equation for the delivery time is ttotal = tcyc + tcook. There are two terms on the right hand side: tcyc for the cycling time, and tcook for the cooking time. You can make the job of working out the total time, ttotal, easier for yourself by thinking about tcyc and tcook one at a time.
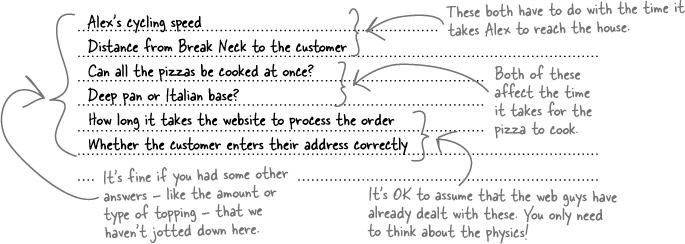
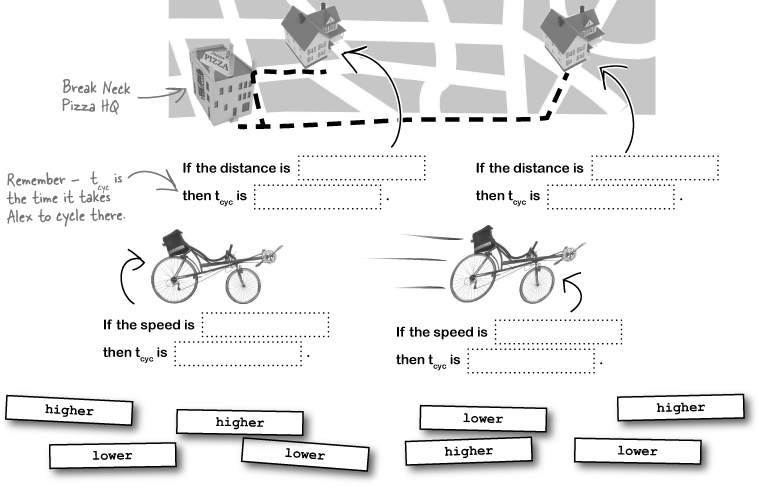
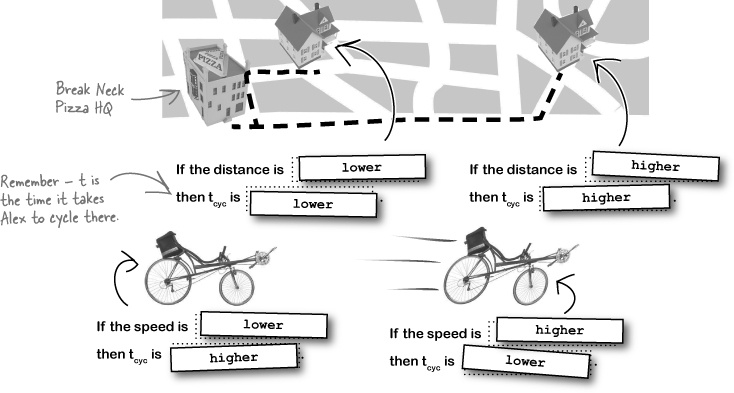
You already made great progress with tcyc (Alex’s cycling time) when you intuitively realized that tcyc must depend on the speed at which Alex cycles and the distance the customer’s house is from Break Neck. But how do the speed and distance affect the cycling time?
What do you expect to happen for extremes, like a short distance or a high speed?
Note
Part of your Sharpen answer from Sharpen your pencil Solution.
Your job is to use the magnets to explain how the distance to the house and the speed at which Alex cycles affect the time it takes him to get there. There are only two words on the magnets, but they all have a place on the pictures.
Your job is to use the magnets to explain how the distance to the house and the speed at which Alex cycles affect the time it takes him to get there. There are only two words on the magnets, but they all have a place on the pictures.
When you start, it helps to be a part of it and think about what happens at different extremes.
Before you start trying to work out what’s going on with numbers and actual measurements, it’s always a good idea to be a part of it. Use your intuition to think about what you expect to happen to the cycling time at certain extremes, like a long distance or a high speed.
If you already have a good idea about how the distance and speed affect the time, you’re more likely to spot any little mistakes you make in your math.
Joe: Well, I guess we could get him to cycle to each potential customer’s house in his area, one house at a time, and set up a database. So when the customer types in their address, the website can look it up in the database and give out a delivery time.
Frank: Think of the overtime that’d cost us! It’d take forever for him to do all that. And he wouldn’t even be delivering pizzas; he’d just be recording times to the houses of people who might never order a pizza...that doesn’t sound like a good idea at all.
Joe: OK. Maybe we could work out an equation for Alex’s cycling time. We already know that t depends on his speed and the distance, so we’d be angling for something that looks like “t = something to do with speed and distance.”
Frank: Ooh, actually, working out the distance to each house is fine. The web guys can already do that with their online mapping gizmo.
Joe: We now need to work out Alex’s speed, so we can try to use it in an equation. I know this sounds weird ... but we might try being Alex. Putting yourself in someone else’s shoes is supposed to help you solve problems.
Frank: Like “Alex pushes the pedals, and the bike goes forward”? OK, let’s brainstorm. So say I’m Alex, out delivering pizzas all evening. I don’t want to ride too fast, or I’ll get tired.
Joe: But I also don’t want to ride too slow, or I won’t deliver that many pizzas and won’t get as many tips.
Frank: But I’m the top delivery guy, so I have the experience to start off riding at the best speed and to keep up that speed for the whole evening.
Jill: So Alex always rides at the same speed. Hmm, if we can work out his speed, could we use that and the distances from the mapping gizmo to work out the time it takes him reach a house?
Frank: I think you might be right. But how on earth are we supposed to work out what speed Alex rides at? And how do we use that to get a delivery time?
It usually helps to BE someone (or something), so you see what the physics looks like from inside the problem.
Brain Power
How might it be possible to measure Alex’s speed, so you can use it to work out cycling times for deliveries?
Joe: Well, if Alex always rides at the same speed, he should always cover the same distance in the same amount of time.
Frank: Ah ... I think I see what you mean. If Alex always goes at the same speed, and we measure his time for 1 km, it’ll always take him that amount of time to cycle 1 km. But wouldn’t we still need to time him over all possible distances to keep our bases covered?
Joe: I don’t think we need to time Alex over lots of distances. If we time how long it takes him to cycle 1 km, we know, without having to time him again, that it’ll take him twice as long to go 2 km.
Frank: Then, we can take his time for 1 km and say it’ll take him half as long to go 0.5 km, and three times as long to go 3 km. I get it! So we only need to time him once to get his time for any distance.
Jill: I’m not so sure about only timing him once. A lot hangs on this- if we get the delivery times wrong, the customers get free pizza, and that’s very expensive. Why don’t we time him more than once over 1 km and take an average of all his times in case there’s a bit of fluctuation between one run and the next?
Joe: A bit of uncertainty, you mean? That makes sense. And why don’t we cover our bases by timing Alex over a variety of distances to make sure he does always ride at the same speed?
Jill: Sounds good to me.
Frank: Aren’t we giving ourselves a harder calculation to do at the end though? If we just time Alex once over 1 km, it’s easy to scale the time for a different distance - 2 km takes twice as long, 0.5 km takes half as long, and so forth. If we time him more than once over a variety of distances, how can we work them out?
Jill: If we work out Alex’s speed in meters per second, we can use that to work out the time. So suppose he goes at 10 m/s; he’d cover 100 m in 10 s, 1 km in 100 s, and so on. We can estimate his time for any distance if it follows the same pattern.
Frank: OK, I think you’ve managed to convince me - especially since the town is relatively flat, so there aren’t any hills to mess things up. Let’s go design an experiment!
When you do an experiment, you should make multiple measurements so you get the best average possible.
Making multiple measurements gives you an idea of how widely your results are spread out.
At the moment, you’re assuming that Alex always rides at the same speed. But what if he doesn’t, or if his speed varies between trips or at different distances?
If you only time Alex once, you have no idea how consistent his speed is. If you time him more than once, and his results have a wide spread, then you’ll probably need to think again. But if his times are all similar to each other and close to the margin of error of your stopwatch, then you’re good to go with their average.
When you design an experiment, think about what might go wrong!
Making more than one measurement is just one way of improving your experiment. Everything in your experiment - Alex, the road, your tape measure, and your stopwatch - could cause you problems! If you don’t think about the worst that could happen before you start, you could end up with useless results and no chance to repeat the experiment.
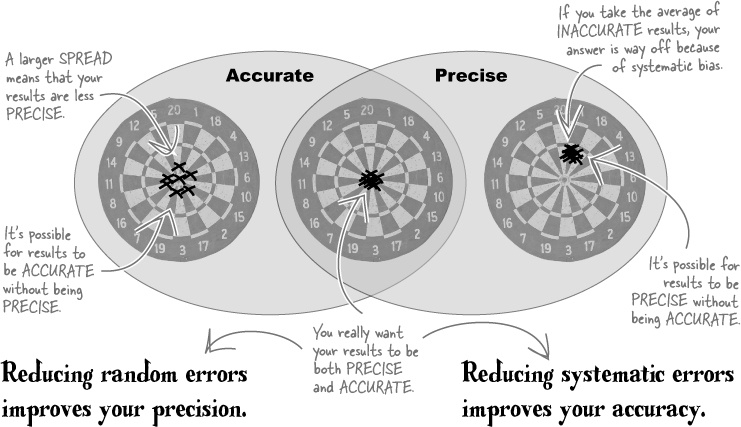
There are two different types of errors-random and systematic.
You already realized that if Alex’s speed isn’t 100% consistent, his times will be spread around. This is similar to the range that a measurement may fall into due to your measuring device having scale divisions (like your myPod measurements). If Alex’s times aren’t too different for each ride, you can reduce the random error by making several measurements and taking an average.
Some sources of error are built into the system. If you time Alex going downhill, he will be faster than he would around the town, which is mostly flat. If the tape measure has stretched, the actual distance will be shorter than you think it is. Errors like these are called systematic errors, and they bias the results in one particular direction. Taking averages doesn’t help reduce bias, as all the results will be higher (or lower) in the direction of the bias. You need to spot them in advance and plan ahead to minimize them.
Random errors involve SPREAD. Minimize them by AVERAGING.
Systematic errors involve BIAS. Minimize them by PLANNING ahead.
OK - time to recap where you’re at...
You’re designing an experiment to help Break Neck Pizza with their website, on a spare napkin (as all good physicists do), but unfortunately, some of the words have succumbed to pizza grease.
Fill in the blanks using the words at the bottom of the box.
Missing words: | speed, three times, extrapolate, direction, systematic, distance, once, repeat, average, time, distances, random, flat, times |
Conduct an experiment to find out Alex’s speed
You need to give Break Neck Pizza’s customers a delivery time. It’s important not to get this wrong since you’ll have to give out free pizza if you do!
You’ve decided to do an experiment to find out Alex’s speed when he’s out delivering pizzas. Then you can use that to work out the time it takes him to cover any distance.
You’re timing Alex over three different distances, three times for each distance. That way you’ll be able to spot how consistent Alex’s speed is and smooth over random errors. These crop up because you can’t recreate exactly the same conditions each time, and because your measuring devices can’t possibly be accurate to the nearest fraction of an atom! You’ve also thought of possible sources of systematic error and made sure your equipment is up to scratch.
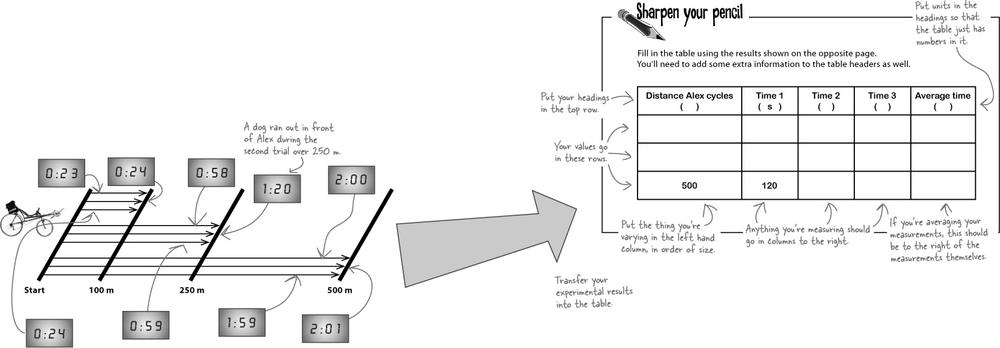
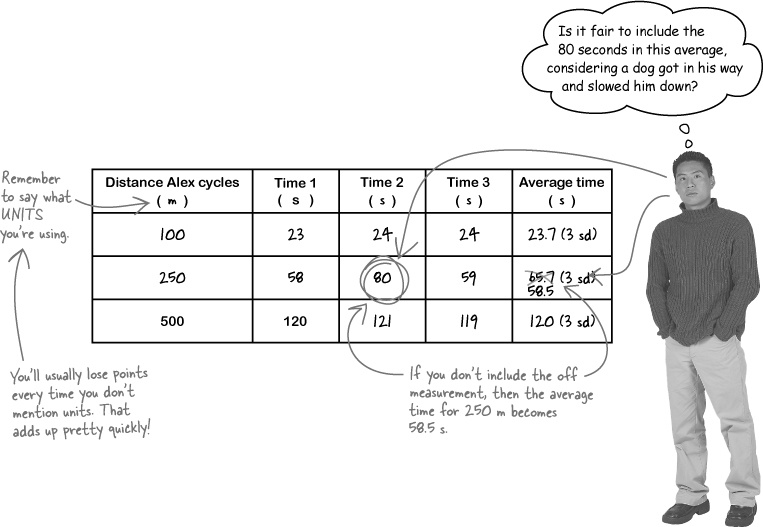
Write down your results... in a table
As you’re doing your experiment, write your results down in a table. This keeps all your related pieces of information next to each other, in rows or columns. You’re less likely to make a mistake writing down a measurement if you use a table. It’s also much easier to see what’s going on and spot patterns in your experiment
The headings for your table should go in the top row, with the thing you’re changing on the left, and the thing(s) you’re measuring to the right. You should put the units of each column in the headings.
As you make measurements for your experiment, write them down in a TABLE.
Tables help you keep your results ordered and make it easier for you to spot patterns.
Fill in the table using the results shown on the opposite page. You’ll need to add some extra information to the table headers as well.
Look out for measurements that don’t fit.
One of the reasons for timing Alex more then once over each distance was to assess the spread (or scatter) of his results. If he can’t ride at a consistent speed, you’ll have to think again about your whole approach.
In this experiment, all of the times for each distance are close together, with a spread similar to your stopwatch’s margin of error. However, there’s one time that’s way off. The 80 s measurement for Alex going 250 m sticks out, and you need to think about why. Is it because Alex isn’t very consistent - or did something go wrong just that one time?
If the measurements are spread out because Alex is inconsistent, you should probably make more and more measurements at each distance, so you can get a better idea of the spread and take a better average.
If there’s a good reason for the outlying data (which there is here because a dog ran out in front of him), then it’s OK to discard the measurement since it’s not representative.
Note
Thinking about where your outliers may have come from will help you to improve your experimental setup and reduce errors.
If a measurement doesn’t fit, think about WHY it doesn’t before deciding what to do with it.
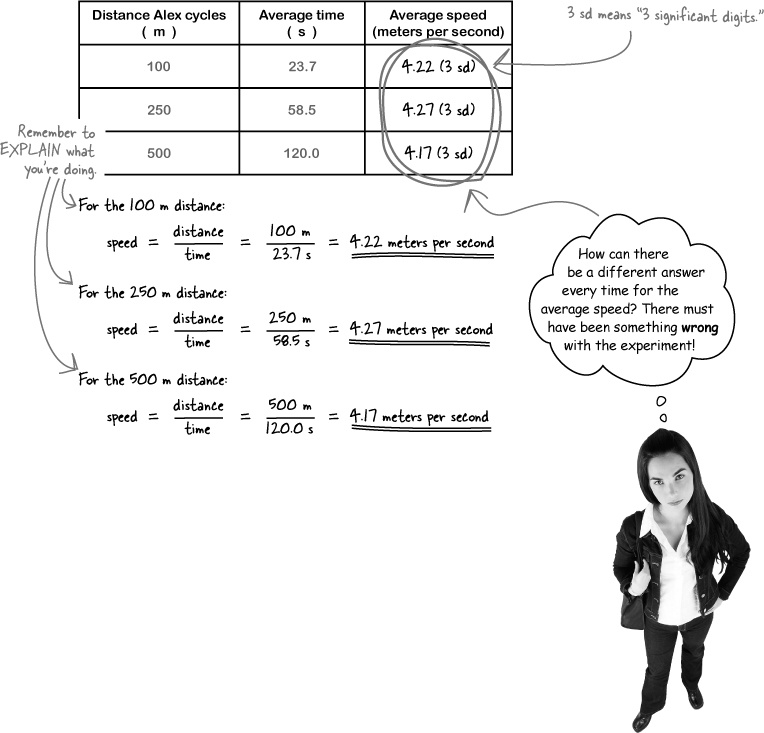
Use the table of distances and times to work out Alex’s speed
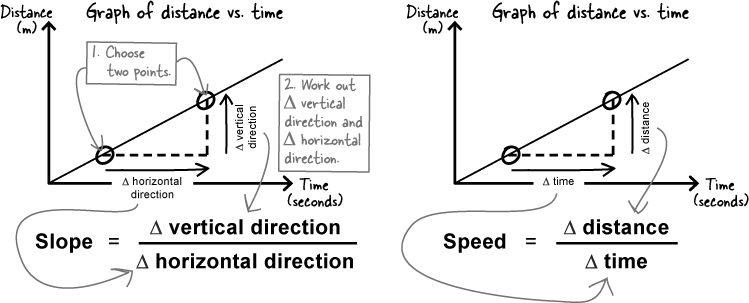
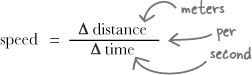
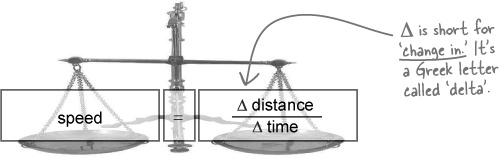
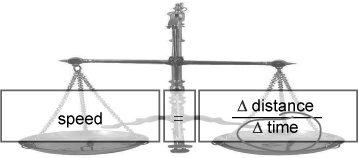
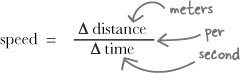
Now that you have a table of distances and times, you can work out Alex’s speed. Speed is measured in miles per hour, kilometers per hour, or meters per second. “Per” means “divided by,” so whatever the units, the dimensions of speed are distance divided by time. And the speed itself is the change in the distance Alex has gone since he started divided by the change in the time that’s gone by since he started.
Note
Don’t worry too much about the ‘change in’ bit for now. You’ll see why it’s really important later on in the chapter.
Once you’ve worked out Alex’s speed, you can give the customer a delivery time for any distance.
You can work out the equation for speed using its UNITS -“miles per hour,” “kilometers per hour,” and so on. Speed is distance divided by time.
Note
Strictly speaking, this reasoning only works for simple equations. But here you intuitively know it’s right.
It’s OK - there will be some spread in your experimental results due to random errors.
For a start, the error on each of your measurements is ± half a scale division. Then there are random fluctuations in things you don’t have control over - tiny changes in wind speed, the exact state of Alex’s tires, tiny changes in the surface of the road, and so on.
When you measure the same thing more than once, you shouldn’t expect exactly the same answer each time.
Random errors mean that results will be spread out
Random errors mean that your experimental results will be spread around an average. If they’re not spread out very much, your results are said to be precise.
However, if you have an underlying systematic error that’s biasing your results in one particular direction (like if the stopwatch is consistently started at the wrong time), then you won’t be able to work out an accurate value by taking an average.
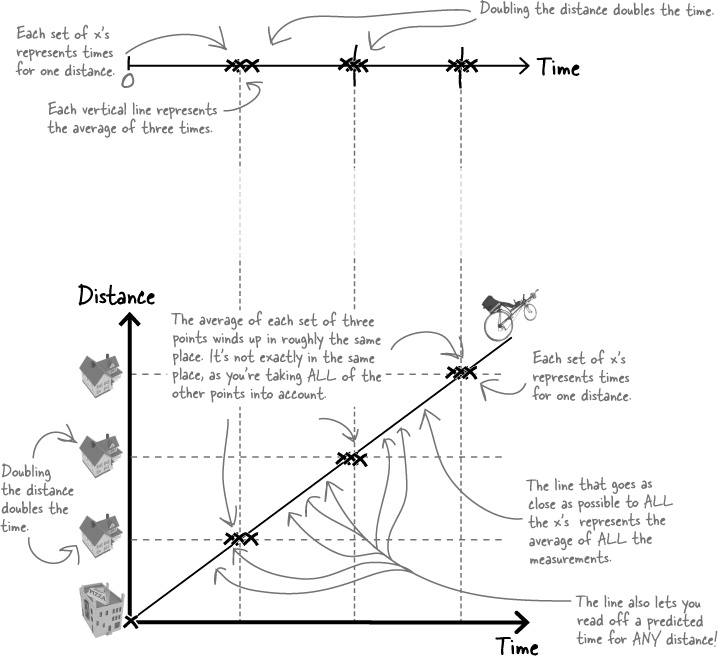
A graph is the best way of taking an average of ALL your results
So far you’ve been taking the average of one set of results at a time - but the average times (and, therefore, average speeds) for each distance are slightly different. You can kind of think of this as a ‘one-dimensional’ average.
The best way to work out the average speed across all of your results is to draw a graph. Since you’re expecting the time to double every time you double the distance, triple every time you triple the distance, and so on, your measurements will lie along a straight line. You can kind of think of this as taking a ‘two-dimensional’ average, as you’re using two axes for your plot and are able to include measurements made for different distances on the same graph.
This also has the advantage of giving you a way of reading off the time it should take to cover any distance.
As is often the case in physics, a picture speaks a thousand words!
You’ve probably drawn graphs before, so here’s a quick refresher.
The most important thing is to make it clear what your graph is representing! That means you need a title, labels for each of your axes, and units along each axis.
Plot your points by putting the center of an ‘x’ exactly where your measurement is.
If you’re expecting each thing you’ve plotted to double when you double the other thing, draw the best straight line you can through all the points on your graph. This takes the best average possible of all your data and allows you to read off extra values by interpolating (for values that lie between your measurements) or extrapolating (for points that lie beyond the range of your measurements).
This graph isn’t of the experiment you did with Alex - that’s your job on the next page! It’s another graph where the doubling thing happens - the cost vs. volume of pizza sauce!
Plotting your measurements on a graph helps you take a better average than before.
The first time around, you took a separate average of Alex’s times for each distance. But you got a different answer for each distance - not a great result.
By doing multiple measurements over more than one distance in the first place, you increase the precision of your result by reducing random errors. But if you don’t somehow combine all these results together to get one answer, you’re not answering the question completely.
If you plot the points on a graph and draw the best-fitting straight line you can, then you’re using all of them to take an average - a much better way of doing things.
And because it’s visual, you’ll be able to see if any of your points are outliers.
Fitting a line to a graph is like taking an ‘informed average.’
Use a graph to show Alex’s time for ANY distance
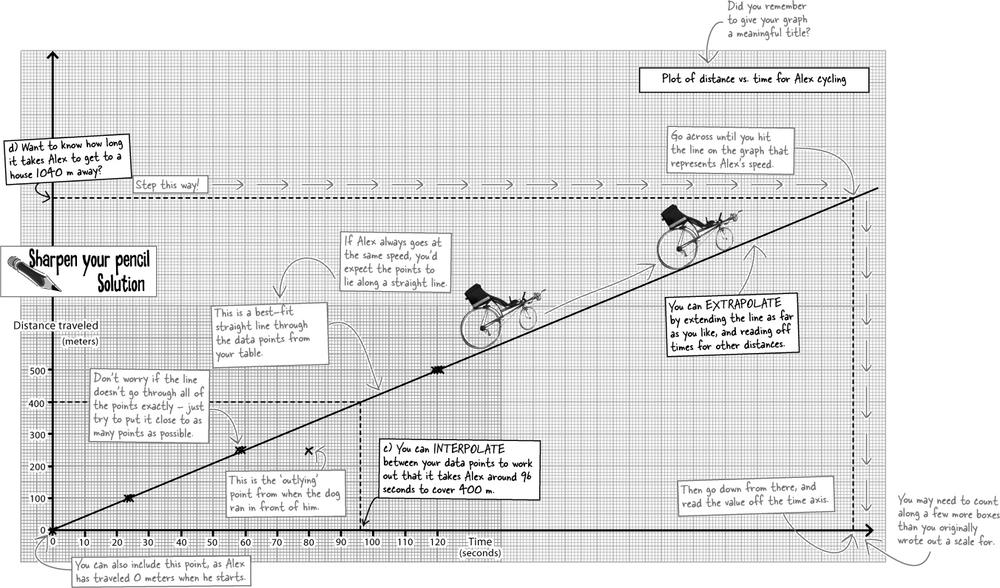
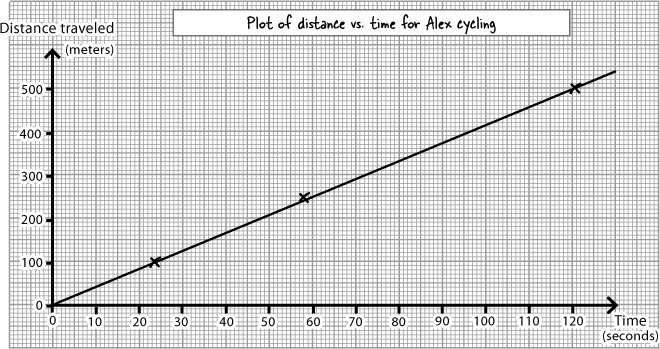
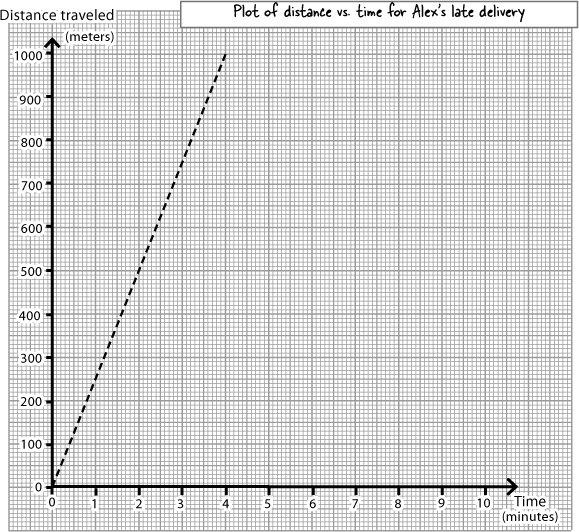
Alex is good at sticking to the same speed. This means that if you double the distance, then the time he takes to cover the new distance will double accordingly.
In other words, the distance and time points should lie along a straight line when you plot them on a graph (give or take experimental error). And once you’ve plotted a graph, you can read off Alex’s time for any distance.
Distance Alex cycles (m) | Time 1 (s) | Time 2 (s) | Time 3 (s) |
100 | 23 | 24 | 24 |
250 | 58 | 80 | 59 |
500 | 120 | 121 | 119 |
a) Plot the measurements from the table as points on the graph (you can skip the outliers).
b) Then draw a best fit straight line through the points so that you can read off the time it’ll take Alex to travel any distance.
c) How long do you think it’ll take Alex to travel 400 m?
_________________________________________
d) And how would you work out his time for a house 1040 m away?
_________________________________________
_________________________________________
The line on the graph is your best estimate for how long Alex takes to cycle ANY distance
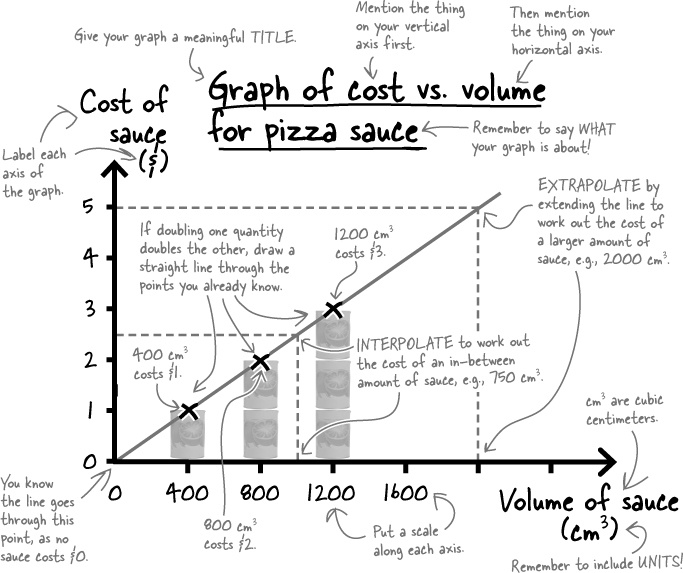
Now that you’ve drawn a graph, you can use it to read off ANY distance Alex may have to travel by extending the straight line you drew, and estimating the pattern or extrapolating from that.
So for example, if a house is 1040 m away (much further than any of the distances we got Alex to bike in the experiment), you can extend the graph and straight line to find out that it would take him 250 seconds to get there. The graph works!
There’s only one problem - how to get the graph “into” the Break Neck website, so it can give the time to the customer.
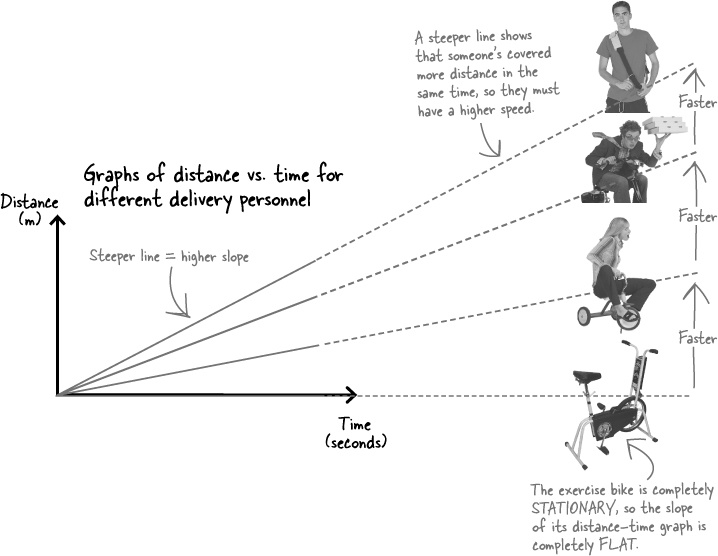
You can see Alex’s speed from the steepness of the distance-time graph
The distance-time graph not only lets you read off values, but it also lets you see how fast something’s going at a glance.
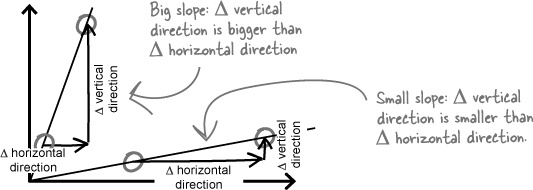
The faster someone is, the greater the distance they go in a set time. When you plot their distance-time graph, you’ll see its slope (or gradient) is steeper compared to someone who’s slower. The higher the speed, the steeper the slope of the distance-time graph.
So if Alex raced against the delivery personnel from some of Break Neck’s rivals (all going at their steady delivery speed), you’d be able to pick the winner in advance from the slope of their distance-time graphs.
In physics, the steepness of a graph is called its SLOPE.
The faster something’s going, the steeper the slope of its distance-time graph.
You can only compare the slopes of graphs by eye if they have the same scale.
All the graphs on the opposite page have the same scale. This means that you can just see who’s going the fastest, as their graph has the steepest slope.
Note
This is being qualitative, like saying “this one’s faster” or “this one’s slower” but without mentioning any numbers.
But if you have one graph where 1 cm on paper = 200 m in real life and another where 1 cm = 10 m, then a line representing the same thing will look very different.
However, a delivery person will still cover the same distance in the same time no matter which scale you use for their graph. So the distance on their graph will still change by the same number of meters in the same time. Whatever scale it’s drawn at, the numbers don’t change, and you can calculate a value for the slope.
To be quantitative, you have to calculate the slope of your graph using numbers.
If you calculate the slope of your distance-time graph, it’ll give you an equation which will show you how the distance and time relate to each other. And as Alex’s speed is (change in) distance divided by (change in) time, you’ll be able to work that out. This is what you really want for the Break Neck Pizza website!
Note
This means doing things with numbers (so that the website can give the customer a delivery time).
When you calculate the slope of a graph, you get an equation which shows you how the two things you plotted on the graph relate to each other.
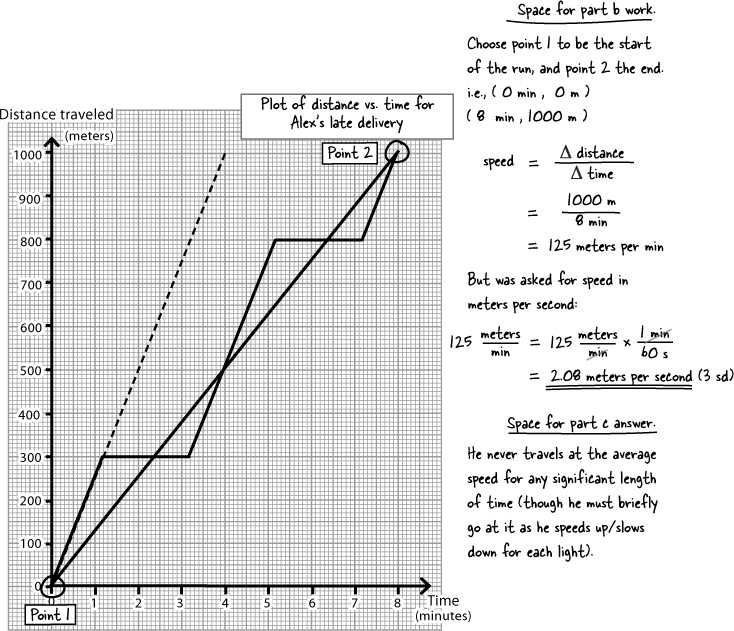
Alex’s speed is the slope of the distance-time graph
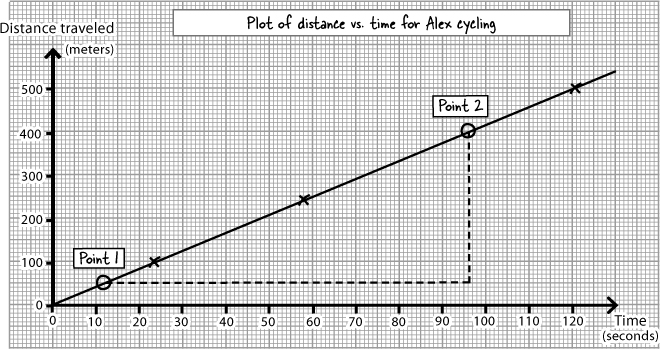
To calculate the slope of a straight line graph, pick two points on it, and work out the change in the vertical direction divided by the change in the horizontal direction. The steeper the graph, the larger the slope.
On your graph, the vertical axis is distance, and the horizontal axis is time. So the slope of your graph is change in distance divided by change in time - exactly the same as your equation for Alex’s speed.
To save time, you can use shorthand ‘Δ’ which means “change in.” So “change in distance” is Δ distance.
Now work out Alex’s average speed from your graph
a. Choose two points on the line, and calculate the slope of the distance-time graph. Use the tips on the opposite page to help you.
b. What do you notice about the units of your answer?
a. Choose two points on the line, and calculate the slope of the distance-time graph.
b. What do you notice about the units of your answer?
Point 1 is (12s, 50m), Point 2 is (96s, 400m)
The units of the slope (meters per second) are the same as the units for speed – distance divided by time.
This makes sense, as the equation for slope of the graph is the same as working out the distance covered per amount of time. The slope of the distance-time graph is the speed!
You need an equation for Alex’s time to give to the web guys
You’ve used the results of your experiment to draw a distance-time graph and calculate its slope, which is the same as Alex’s speed. That’s fantastic!
But the web guys need to be able to use Alex’s speed and the distance to a house to work out the time it takes Alex to get there. And they’re asking you for an equation that they can plug the distance and speed into to get the time.
You already have an equation that involves speed, distance, and time, which you worked out from the units of speed:
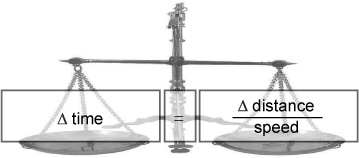
This gives you the average speed at which something travels between two points. But the equation says “speed = ” on the left hand side, allowing you to work out a speed if you know a distance and a time. What the web guys want is an equation that says “ Δ time = ” on the left hand side, so they can work out a time from the map distance and Alex’s speed.
How are you going to get an equation that the web guys can use?
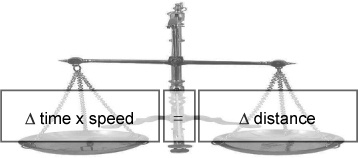
Rearrange the equation to say “Δ time = something”
If you have an equation where the thing you want isn’t on the left hand side all by itself, you’ll have to rearrange the equation so that it is.
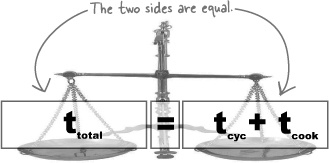
The top thing to remember when rearranging equations is that you must do the same thing to each term on both sides of the equation or else the two sides won’t be equal (or balance) anymore. The huge advantage of this is that you don’t have to remember lots and lots of equations, as you can rearrange the ones you know to figure out what you need.
Note
For time, speed, and distance, you only need ONE equation, which you ALREADY know (from the units of speed).
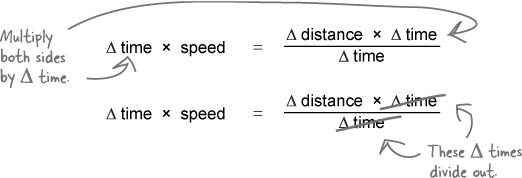
You can rearrange your equation to say “Δtime = something” like this:
At the moment you’re dividing by Δ time. You want an equation that says “Δ time = something.” So multiply both sides by Δ time to get it off the bottom.
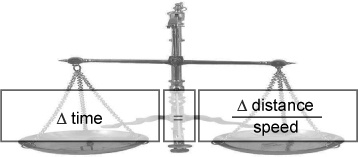
You now have Δ time where you want it, but at the moment it’s being multiplied by speed. So divide both sides by speed to sort that out.
When you rearrange an equation, always make sure you do the same thing to each side so that the equation remains BALANCED
An equation that says ”Δ time = something” that you can use for the Break Neck website. Sorted!
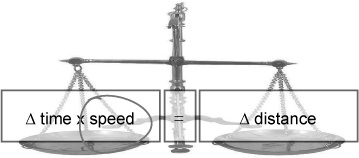
At the moment you’re dividing by Δ time. You want an equation that says “Δ time = something.” So multiply both sides by Δ time to get it off the bottom.
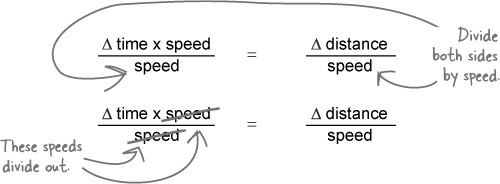
You now have Δ time where you want it, but at the moment it’s being multiplied by speed. So divide both sides by speed to sort that out.
An equation that says “Δ time = something” that you can use for the Break Neck website.
When you rearrange an equation, show your work ...
Math is the main tool you use to communicate ideas and make predictions in physics.
A large part of physics is understanding the physical principles behind things. And to an extent you’re right - you can do reasonably well in high school physics by understanding some principles and rote-learning a few equations.
But when you step up a level to AP Physics, there are far too many potentially useful equations and relationships for you to be able to memorize them all, never mind every single way they can be rearranged. And you need to be able to use the principles to make concrete predictions - for example, the time it’ll take Alex to cycle a particular distance. And that has to involve math.
This chapter is all about learning to use graphs and equations, two universal languages of physics. Like any language, math can be difficult to get used to at first. But with practice, you’ll get used to communicating the physics principles with it. More than that - as you move on, the math enables you to understand and visualize difficult physical principles and concepts.
At AP level, being able to rearrange equations yourself is a must, so stick at it. The rewards are massive, as you’ll only need to learn relatively few fundamental equations, which you can then rearrange to get any other equation you might need. Thinking like a physicist isn’t about rote memorization. So hang in there - it will get easier!
In physics, math is a vital tool for making predictions and communicating principles.
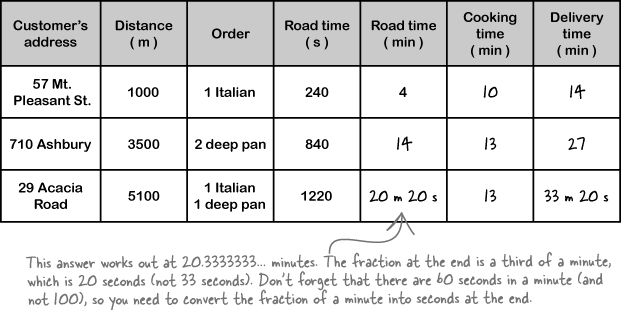
Use your equation to work out the time it takes Alex to reach each house
You now have an equation that lets you predict how long it takes Alex to get to each of Break Neck’s potential customers!
First, you designed and carried out an experiment. After looking at the results to see how spread out they were, you plotted the results on a graph, drew a best-fit straight line, and calculated the slope of the line to find Alex’s speed in terms of the change in distance and change in time. Phew!
And you’ve just rearranged the speed equation so that you can put in a speed and distance to calculate the time it takes Alex to travel that distance at that speed:
So now you can do a test run with some random addresses to catch any potential problems before the site goes live.
A ‘test run’ is an important part of seeing if your answer’s correct.
So you do a test run with the website ...
... but there’s a problem. The programmers set the website up to display delivery times in units of minutes. Your calculation used seconds, but the units weren’t converted before being displayed.
Doing the question right, but giving the wrong UNITS in your answer is a common, but avoidable, error.
So just convert the units, and you’re all set...right?
Not so fast! Any time you think you’re ready to roll with an important website (or even an answer on your exam), take a look from 20,000 feet away and ask yourself: Does this SUCK?
You’re never finished until you’ve asked: “Does it SUCK?”
SIZE - Are the answers the size you’re expecting? _____________________________________ _____________________________________ | |
UNITS - Do they have units, and are they what you were asked for? _____________________________________ _____________________________________ | |
CALCULATIONS - Did you do the math right? _____________________________________ _____________________________________ | |
“K’ONTEXT - What are you trying to do, and is it the same as what you actually did? _____________________________________ _____________________________________ |
Change the units for this customer’s delivery time to minutes, then step back to see if it SUCKs.
SIZE - Are the answers the size you’re expecting? Well, 4 minutes is plausible for pizza delivery in a way that 240 minutes isn’t! _____________________________________ | |
UNITS - Do they have units, and are they what you were asked for? They asked for minutes, and they’ve got minutes. (Well, they do now!) _____________________________________ | |
CALCULATIONS - Did you do the math right? The first equation I wrote down was ttot = tcyc + tcook, where tcyc was the cycling time, and tcook the cooking time. OH NO, I FORGOT ABOUT THE COOKING TIME!! | |
“K’ONTEXT - What are you trying to do, and is it the same as what you actually did? Apart from using the wrong units originally, and forgetting the cooking time, I think the rest is OK. |
Doing part of the problem right, then writing the ‘interim’ answer to that part as your final answer by mistake is another common (and very avoidable) error!
Include the cooking time in your equation
The original equation included both a delivery time and a cooking time. You did a fantastic job of working out the hard part - the delivery time - but forgot to add on the cooking time at the end.
The Break Neck website goes live, and the customers love it!
You’ve done it! Break Neck have a shiny new website thanks to your experiment, graph, equation, and units conversion. Every time a customer makes an order, they’re given a delivery time that they can plan their evening around.
The customers are delighted, and word’s starting to get around. Alex is pleased too. He’s getting more tips and has nearly saved up enough for the new myPod he has his eye on.
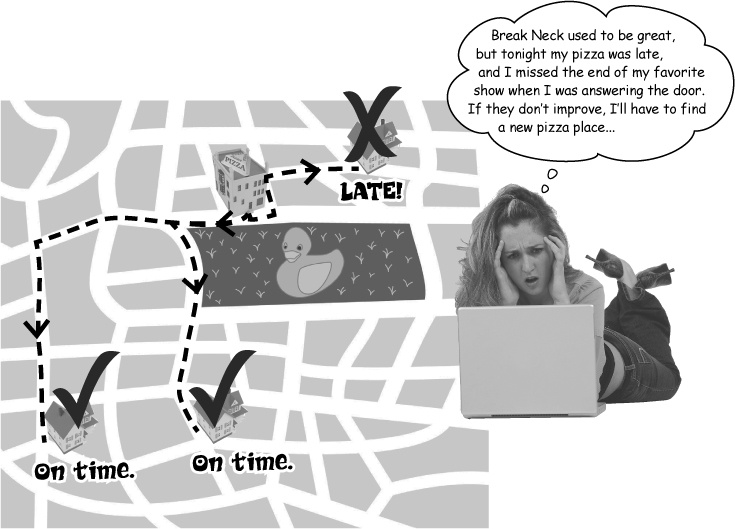
A few weeks later, you hear from Break Neck again
Most of the pizzas are still arriving on time ... but some of the pizzas are late, and the customers are starting to get impatient with Break Neck. The worst thing that could happen would be customers switching to one of Break Neck’s competitors because of a bug in the website.
So Break Neck has asked you to come back on a new contract to see if you can work out what the problem is.
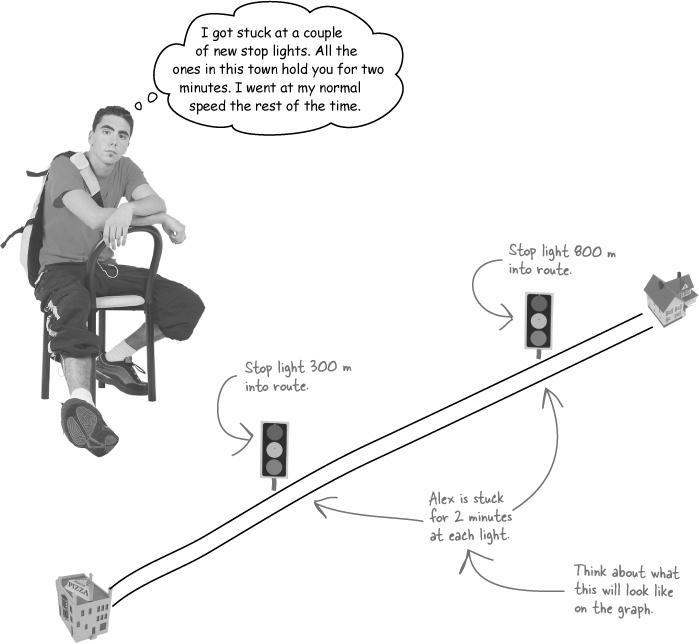
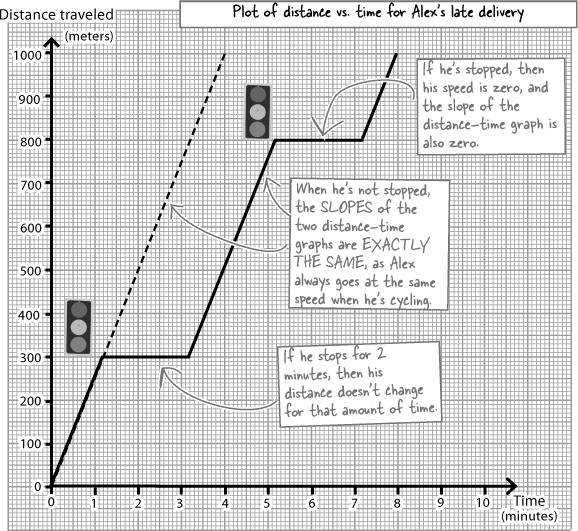
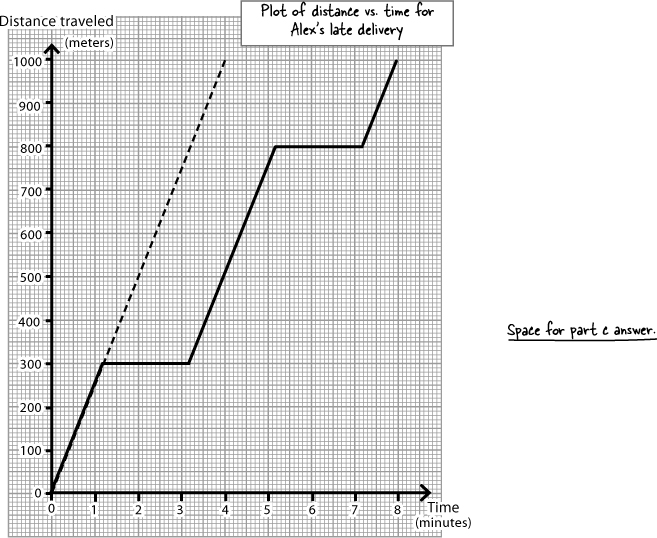
A graph lets you see the difference the stop lights made
If you can see the difference the stop lights made to Alex’s journey, you’re more likely to be able to work out what to do about it.
The line already on the graph represents what we expected Alex to do - travel at a constant speed without stopping, so he reaches the house in four minutes.
Draw Alex’s actual journey (which he describes over there on Brain Power) on the graph to show and compare the difference that the stop lights made.
The line already on the graph represents what we expected Alex to do - travel at a constant speed without stopping, so he reaches the house in four minutes.
Draw Alex’s actual journey (which he describes over there on Brain Power) on the graph to show and compare the difference that the stop lights made.
It’s easy to tell when something’s sitting still, as the slope of its distance-time graph is zero (or a flat line).
The stop lights change Alex’s average speed
The average speed for a trip is the constant speed at which you could have traveled to cover the same total distance in the same total time. So Alex’s average speed is the slope of a line between his start and end points on his distance-time graph since the slope of a distance-time graph is the speed.
With an AVERAGE speed, it’s the changes in total distance and total time that are important.
Add on two minutes per stop light to give the customer a maximum delivery time ...
Note
Trying to do something with the average speed will be too difficult at this stage; this is simpler.
In physics, simpler is usually clearer - and, therefore, better!
So you - and Alex - have reached the end of the road. You realized that the stop lights slow him down. But you were able to get the online map to consider the number of stop lights on his route when giving the customer a maximum delivery time.
If the lights are red, that’s OK because you planned for that to happen. If the lights are green, and Alex isn’t slowed down, then the pizza arrives early, and the customer is still happy.
...and you’re invited to the Pizza Party
If you understand physics, you don’t have to memorize equations!
Physics isn’t about learning equations. Physics is fundamentally about the world around you.
When you’re trying to work stuff out with physics, it usually involves making measurements, then drawing graphs and/or writing down equations that show you how varying one thing (like the distance to a house) changes something else (like the delivery time for a pizza).
Yes, there’ll be some equations that you’ll have to learn to get by - but only a few. Most of the ones in this book are equations that you can work out from the general physics principles you’re learning. Remember - put yourself into the heart of the problem, then use what you already know! Use your intuition and graphs to see whether you expect something to get bigger or smaller when you change another thing.
In physics, memorizing is the opposite of understanding!
If you see it, you get it!
You already knew the two equations you’ve used in this chapter!
The first equation you used was:
But that was something you already knew! Every time you say something has a speed of “70 miles per hour,” you’re quoting units that you can use to write down that equation straight out of your head!
The second equation you used was:
But you already knew that one too! Steep hills have big slopes. So you can use your intuition to work out that Δ vertical must be on the top of the fraction so that you get a big value for a big slope.
A steep hill has a big slope.
Question Clinic: The “Did you do what they asked you” Question
Distance | A length; the number of meters (or miles, or so forth) you cover when you take a particular route between two points. | |
Time | How long something takes; how many seconds (or minutes, and so on) that elapse between two moments you’re interested in. | |
Speed | How fast something’s going - the rate of change of distance with time. | |
Graph | A visual representation of how two variables depend on each other. | |
Equation | A mathematical representation of how variables depend on each other. | |
Slope | The steepness of a graph; the change in the vertical direction divided by the change in the horizontal direction. |
Your Physics Toolbox
You’ve got Chapter 4 under your belt, and you’ve added some terminology and answer-checking skills to your toolbox.
Get Head First Physics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
