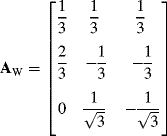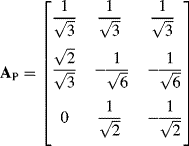High Performance Control of AC Drives with Matlab / Simulink Models

9.2 Three-phase to Two-phase Transformations

For a deeper analysis of electric drives with filters, knowledge of filter models is required.

The natural frame of co-ordinates for a three-phase system is a three-axis co-ordinate with a 120-degree shift, but for a better analysis of the system, the use of the orthogonal co-ordinates is more useful, as well as easier to understand. Therefore, for the next analysis, proper co-ordinate transformations are presented. Two kinds of transformations are used, one for constant vectors magnitudes and another for constant power of the three-phase and two-phase frames of reference.

The transformation matrix for the conversion from a three-phase ABC co-ordinate to a two-phase αβ0 co-ordinate for constant vector magnitude is described as

(9.1)

and the transformation matrix for constant power of the system is

(9.2)

Using equations (9.1) or (9.2), each of the model variables x can be transformed from ABC to two-phase αβ0 co-ordinates according to

(9.3)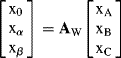

where the variables retain the same magnitude in each co-ordinate.

The next relation is used when the constant power of both systems is fulfilled:

(9.4)

The parameter transformations are required for ...