Chapter 10Theta
Theta (θ or for the capital letter Θ) is the change of the value of an option in relation to the change in time, also called time-decay.
It is the derivative of the value in relation to time, mathematically: 
. Throughout the book the Greek letter Θ will be used for denoting the theta, sometimes time decay will be used. The formula for calculating it is as follows: 
(interest rate and dividend yield at 0%), where 
is the probability density function. Theta has a log normal distribution.
The theta, as shown in Chart 10.1, is expressed in dollars (or rather cents) per day. The theta value indicates the amount with which the value of an option will decrease overnight. An option will get cheaper every day towards maturity. At expiration date the option (when not in the money) has lost all of its value, each time decreasing in value at a daily time decay rate.
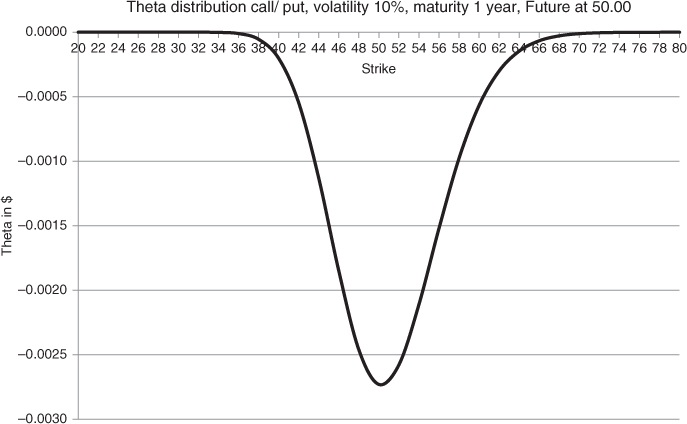
Chart 10.1 Theta distribution call/put, Future at 50, volatility at 10%, maturity 1 year
When the interest rate and the dividend yield are both at 0%, theta for calls will be the same as theta for puts. Theta ...
Get How to Calculate Options Prices and Their Greeks: Exploring the Black Scholes Model from Delta to Vega now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
