Image Reconstruction

Figure 6.22 shows the unit circles using the l2 norm, l1 norm, and l0 quasi-norm, respectively. Except for the l2 norm unit circle, the other two unit circles do not look like circles at all. For a “measure” to be qualified as a norm, it needs to satisfy a set of axioms. A quasi-norm is almost a norm except that it does not satisfy an axiom called the triangle inequality.

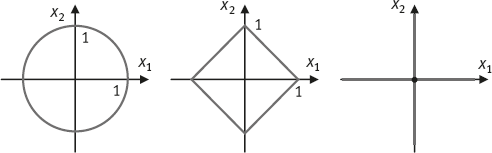
Fig. 6.22: A unit circle is a trajectory of the points that have a distance 1 from the origin. Left: l2 norm’s unit circle. Middle: l1 norm’s unit circle. Right: l0 quasi-norm’s unit circle.

In theory, the l0 quasi-norm is the best measure to promote the sparsity of ψX and should ...