Introduction to Mixed Modelling: Beyond Regression and Analysis of Variance, 2nd Edition

Chapter 11Why is the criterion for fitting mixed models called REsidual Maximum Likelihood?

11.1 Maximum likelihood and residual maximum likelihood

In the preceding chapters, we have established the need for mixed models, that is, statistical models with more than one random-effect term, and have seen how to construct such models and how to interpret the results obtained when they are fitted to data. We have noted that the criterion used to fit a mixed model – that is, to obtain the best estimates of its parameters – is called REsidual Maximum Likelihood (REML), but we have not so far examined the meaning of this term. In this chapter, we will explore the concept of maximum likelihood and its use as a criterion for the estimation of model parameters. We will then show how the criterion for parameter estimation used in the earlier chapters can be viewed as residual or restricted maximum likelihood. The argument will proceed as follows:

• Consideration of a model comprising only the random-effect term Ε. The estimation of its variance 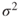using the maximum-likelihood criterion.
• Consideration of the simplest linear model, comprising the fixed-effect term μ and the random-effect term Ε. The simultaneous estimation of μ and 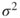using the maximum-likelihood criterion. An alternative estimate ...