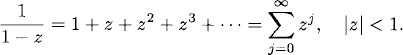APPENDIX A
AUXILIARY MATERIAL
A.1 Some useful Taylor series
We collect here some useful Taylor series used throughout the text, z denotes a complex variable, and the expression on the right denotes the convergence region.
(A.1) 
(A.3) 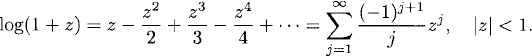
A.2 “ ” notation
” notation
Definition A.1 Let F(x) be a real function. We say that “F(x) is of order f(x) as x tends to a” and write F(x) = ![]() f(x)) as x → a, if and only if there exist two constants C > 0 and δ > 0 such that |F(x)| ≤ C |f(x)| when |x − a| < δ.
f(x)) as x → a, if and only if there exist two constants C > 0 and δ > 0 such that |F(x)| ≤ C |f(x)| when |x − a| < δ.
For example, if F(x) is n + 1 times differentiable around x = a, then by Taylor’s theorem,
![]()
where the remainder term satisfies Rn(x) = ![]() ((x − a)n+1). Here, and many times when it is clear by context, we omit “as ...
((x − a)n+1). Here, and many times when it is clear by context, we omit “as ...
Get Introduction to Numerical Methods for Time Dependent Differential Equations now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.