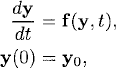CHAPTER 6
SYSTEMS OF DIFFERENTIAL EQUATIONS
In this chapter we motivate, by means of a simple observation, the generalization to systems of equations of what we have learned for scalar differential equations.
Consider the initial value problem for a system of differential equations
where y is an N-component vector and f is an N-component vector-valued function:

The simplest systems are linear systems with constant coefficients:
Here A is a constant N x N-matrix and F has N components.
Let us assume that A has a complete set of eigenvectors; that is, there exists a transformation S that transforms A into a diagonal matrix λ:

Exercise 6.1 The exponential of a matrix A ![]()
![]() NxN is defined via the Taylor series,
NxN is defined via the Taylor series,
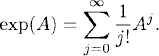
Get Introduction to Numerical Methods for Time Dependent Differential Equations now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.