Introduction to Probability and Stochastic Processes with Applications

CHAPTER 3

SOME DISCRETE DISTRIBUTIONS

In this chapter we present some frequently used discrete distributions.

3.1   DISCRETE UNIFORM, BINOMIAL AND BERNOULLI DISTRIBUTIONS

Definition 3.1 (Discrete Uniform Distribution) A random variable X has a discrete uniform distribution with N points, where N is a positive integer with possible distinct values x_i, i = 1,2, · · · , N, if its probability mass function is given by:

If in particular x_i = i, i = 1,2, · · · , N, the probability mass function is shown in Figure 3.1.

Theorem 3.1 (Properties of a Discrete Uniform Random Variable)If X is a random variable having a discrete uniform distribution with N points, then:

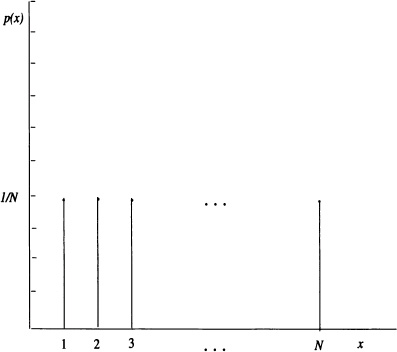
Figure 3.1   Probability mass function for a discrete uniform distribution

1.

2.

3.

Corollary 3.1 If x_k = k, k = 1,2, · · · , N, then:

1.

2.

3.

Proof:

1. Left as an exercise for the reader.
2. Follows from the definition of the mgf. ...