Introduction to Probability and Stochastic Processes with Applications

CHAPTER 9

INTRODUCTION TO STOCHASTIC PROCESSES

In the last eight chapters, we have studied probability theory, which is the mathematical study of random phenomena. A random phenomenon occurs through a stochastic process. In this chapter we introduce stochastic processes that can be defined as a collection of random variables indexed by some parameter. The parameters could be time (or length, weight, size, etc.). The word “stochastic¹” means random or chance. The theory of stochastic processes turns out to be a useful tool in solving problems belonging to diverse disciplines such as engineering, genetics, statistics, economics, finance, etc. This chapter discusses Markov chains, Poisson processes, and renewal processes. In the next chapter, we introduce some important stochastic processes for financial mathematics, Wiener processes, martingales, and stochastic integrals.

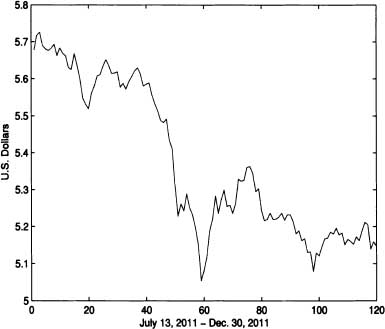
Figure 9.1   Sample path for the U.S. dollar value of 10,000 Colombian pesos

9.1   DEFINITIONS AND PROPERTIES

Definition 9.1 (Stochastic Process) A real stochastic process is a collection of random variables {X_t; t T} defined on a common probability space with values in . T is called the index set of the process or ...